题目内容
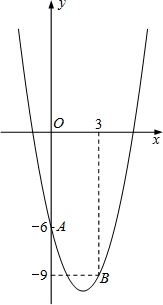 如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).
如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).(1)求出抛物线的解析式;
(2)写出抛物线的对称轴方程及顶点坐标;
(3)点P(m,m)与点Q均在抛物线上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q的坐标;
(4)在满足(3)的情况下,在抛物线的对称轴上寻找一点M,使得△QMA的周长最小.
分析:(1)将A、B点的坐标代入抛物线的解析式中,通过联立方程组求得a、c的值,从而确定该抛物线的解析式.
(2)用配方法将(1)所得抛物线解析式化为顶点坐标式,即可得到其对称轴方程和顶点坐标.
(3)由于点P在抛物线的图象上,那么点P的坐标一定满足该抛物线的解析式,将其代入抛物线的解析式中,即可求得m的值,进而可根据(2)得到的对称轴方程求得点Q的坐标.
(4)△QMA中,QA的长是定值,若其周长最小,那么MA+MQ的值最小,由于Q、P关于抛物线的对称轴对称,若连接AP,那么直线AP与抛物线对称轴的交点必为所求的M点,可先利用待定系数法求得直线AC的解析式,然后联立抛物线的对称轴方程求出点M的坐标.
(2)用配方法将(1)所得抛物线解析式化为顶点坐标式,即可得到其对称轴方程和顶点坐标.
(3)由于点P在抛物线的图象上,那么点P的坐标一定满足该抛物线的解析式,将其代入抛物线的解析式中,即可求得m的值,进而可根据(2)得到的对称轴方程求得点Q的坐标.
(4)△QMA中,QA的长是定值,若其周长最小,那么MA+MQ的值最小,由于Q、P关于抛物线的对称轴对称,若连接AP,那么直线AP与抛物线对称轴的交点必为所求的M点,可先利用待定系数法求得直线AC的解析式,然后联立抛物线的对称轴方程求出点M的坐标.
解答:解:(1)依题意有
,
即
,
∴
;
∴抛物线的解析式为:y=x2-4x-6.
(2)把y=x2-4x-6配方得,y=(x-2)2-10,
∴对称轴方程为x=2;
顶点坐标(2,-10).
(3)由点P(m,m)在抛物线上,
有m=m2-4m-6,
即m2-5m-6=0,
∴m1=6或m2=-1(舍去),
∴P(6,6),
∵点P、Q均在抛物线上,且关于对称轴x=2对称,
∴Q(-2,6).
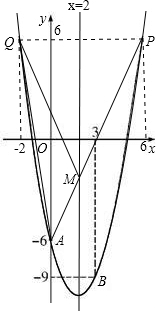 (4)连接AQ,AP,直线AP与对称轴x=2相交于点M,由于P,Q两点关于对称轴对称,由轴对称性质可知,此时的交点M,能够使得△QAM的周长最小;
(4)连接AQ,AP,直线AP与对称轴x=2相交于点M,由于P,Q两点关于对称轴对称,由轴对称性质可知,此时的交点M,能够使得△QAM的周长最小;
设直线PA的解析式y=kx+b,
∴有
,
∴
,
∴直线PA的解析式为:y=2x-6;
设点M(2,n),
则有n=2×2-6=-2,
此时点M(2,-2)能够使得△AMQ的周长最小.
|
即
|
∴
|
∴抛物线的解析式为:y=x2-4x-6.
(2)把y=x2-4x-6配方得,y=(x-2)2-10,
∴对称轴方程为x=2;
顶点坐标(2,-10).
(3)由点P(m,m)在抛物线上,
有m=m2-4m-6,
即m2-5m-6=0,
∴m1=6或m2=-1(舍去),
∴P(6,6),
∵点P、Q均在抛物线上,且关于对称轴x=2对称,
∴Q(-2,6).
 (4)连接AQ,AP,直线AP与对称轴x=2相交于点M,由于P,Q两点关于对称轴对称,由轴对称性质可知,此时的交点M,能够使得△QAM的周长最小;
(4)连接AQ,AP,直线AP与对称轴x=2相交于点M,由于P,Q两点关于对称轴对称,由轴对称性质可知,此时的交点M,能够使得△QAM的周长最小;设直线PA的解析式y=kx+b,
∴有
|
∴
|
∴直线PA的解析式为:y=2x-6;
设点M(2,n),
则有n=2×2-6=-2,
此时点M(2,-2)能够使得△AMQ的周长最小.
点评:此题主要考查了二次函数解析式的确定、抛物线顶点坐标的求法、函数图象上点的坐标意义、平面展开-最短路径等知识点,难度适中.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;