题目内容
【题目】某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
操作发现:
(1)已知,△ABC,如图1,分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE,连接BE、CD,请你完成作图 , 并猜想BE与CD的数量关系是 . (要求:尺规作图,不写作法但保留作图痕迹)
类比探究: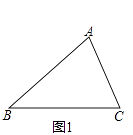
(2)如图2,分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG,连接CE、BG,则线段CE、BG有什么关系?说明理由.
灵活运用: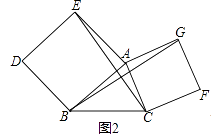
(3)如图3,已知△ABC中,∠ABC=45°,AB=2 ![]() ,BC=3,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.
,BC=3,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.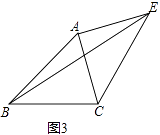
【答案】
(1) ;BE=CD
;BE=CD
(2)
结论:CE=BG且EC⊥BG.
理由:在正方形ABDE和正方形ACFG中,设CE交BG于O,EC交AB于K.
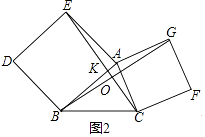
∵AE=AB,AC=AG,∠EAB=∠CAG=90°,
在△ACE和△AGB中,
 ,
,
∴△ACE≌△AGB,
∴CE=BG,∠AEC=∠ABG,
∵∠AKE=∠BKO,
∴∠BOK=∠EAK=90°,
∴EC⊥BG,EC=BG.
(3)
以AB为腰向外作等腰直角三角形Rt△ABG,连接CG.
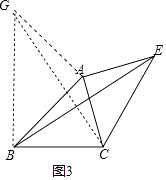
在Rt△ABG中,∵AB=AG=2 ![]()
∴BG= ![]() =4,
=4,
∵∠GBA=∠ABC=45°,
∴∠GBC=90°,
∴CG= ![]() =5,
=5,
∵AG=AB,AE=AC,∠BAG=∠EAC=90°,
∴∠GAC=∠EAB,
在△GAC和△EAB中,
 ,
,
∴△AGC≌△ABE,
∴CG=BE,
∵CG=5,
∴BE=5.
【解析】解:(1)作图如下,
猜想:BE=CD.
理由:∵AB=AD.AC=AE,∠DAB=∠EAC,
∴∠DAC=∠EAB,
在△DAC和△EAB中, ,
,
∴△DAC≌△EAB,
∴CD=BE.
所以答案是BE=CD.
【考点精析】利用等边三角形的性质和正方形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案