题目内容
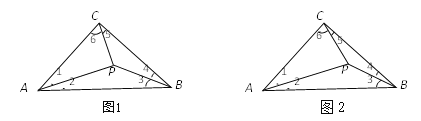
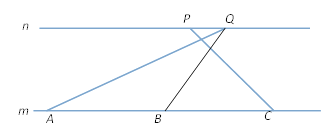
【题目】如图,河的两岸![]() 与
与![]() 互相平行,A、B、C是
互相平行,A、B、C是![]() 上的三点,P、Q是
上的三点,P、Q是![]() 上的两点.在A处测得∠QAB=30°,在B处测得∠QBC=60°,在C处测得∠PCB=45°,已知AB=BC=20米,求PQ的长(结果保留根号).
上的两点.在A处测得∠QAB=30°,在B处测得∠QBC=60°,在C处测得∠PCB=45°,已知AB=BC=20米,求PQ的长(结果保留根号).
【答案】![]() 米
米
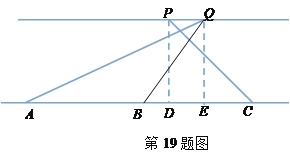
【解析】试题分析:过P、Q分别作PD⊥AC于D,QE⊥AC于E,构造直角三角形,然后解直角三角形即可.
试题解析:如图,过P、Q分别作PD⊥AC于D,QE⊥AC于E,
在△ABQ中,∠QAB=30°,∠QBC=60°,∴BQ=AB=20米,
在直角△BQE中,BQ=20米,∠QBC=60°,
∵![]() , ∴
, ∴![]() 米
米
∴PD= ![]() 米
米
在直角△CDP中,∠PCB=45°,
∴![]() 米,
米,
BD=BC-CD=![]() 米.
米.
在直角△AQE中, ![]() 米,∠QAB=30°,
米,∠QAB=30°,
∵![]() , ∴
, ∴![]() 米
米
∴![]() 米
米

练习册系列答案
相关题目