题目内容
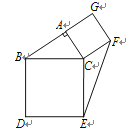
【题目】如图1,菱形ABCD,![]() ,
,![]() ,连接对角线AC、BD交于点O,
,连接对角线AC、BD交于点O,
![]() 如图2,将
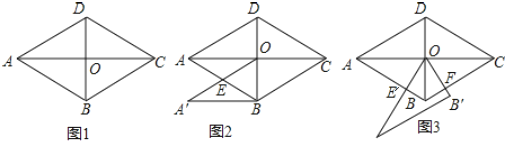
如图2,将![]() 沿DB平移,使点D与点O重合,求平移后的
沿DB平移,使点D与点O重合,求平移后的![]() 与菱形ABCD重合部分的面积.
与菱形ABCD重合部分的面积.
![]() 如图3,将
如图3,将![]() 绕点O逆时针旋转交AB于点
绕点O逆时针旋转交AB于点![]() ,交BC于点F,
,交BC于点F,
![]() 求证:
求证:![]() ;
;
![]() 求出四边形
求出四边形![]() 的面积.
的面积.
【答案】![]() 证明见解析
证明见解析![]()
【解析】
(1)先判断出△ABD是等边三角形,进而判断出△EOB是等边三角形,即可得出结论;
(2)先判断出 ≌△OBF,再利用等式的性质即可得出结论;
(3)借助①的结论即可得出结论.
![]() 四边形为菱形,
四边形为菱形,![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,![]() ,
,
∵AD//A′O,
∴∠A′OB=60°,
![]() 为等边三角形,边长
为等边三角形,边长![]() ,
,
![]() 重合部分的面积:
重合部分的面积:![]() ,
,
![]() 在图3中,取AB中点E,
在图3中,取AB中点E,
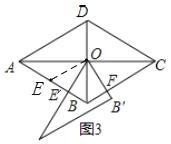
由![]() 知,∠EOB=60°,∠E′OF=60°,
知,∠EOB=60°,∠E′OF=60°,
∴∠EOE′=∠BOF,
又∵EO=BO,∴∠OEE′=∠OBF=60°,
∴△OEE′≌△OBF,
∴EE′=BF,
∴BE′+BF=BE′+EE′=BE=2;
![]() 由
由![]() 知,在旋转过程中始终有△OEE′≌△OBF,
知,在旋转过程中始终有△OEE′≌△OBF,
∴S△OEE′=S△OBF,
![]() S四边形OE′BF =
S四边形OE′BF =![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目