题目内容
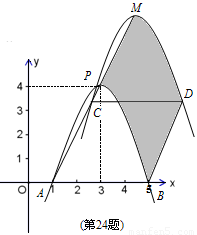
如图,抛物线 经过点A(1,0)和点P(3,4).
经过点A(1,0)和点P(3,4).
1.求此抛物线的解析式,写出抛物线与x轴的交点坐标和顶点坐标,并依此在所给平面直角坐标系中画出抛物线的大致图象;
2.若抛物线与 轴的另一个交点为B,现将抛物线向射线AP方向平移,使P点落在M点处,同时抛物线上的B点落在点D(BD∥PM)处.设抛物线平移前P、B之间的曲线部分与平移后M、D之间的曲线部分,与线段MP、BD所围成的面积为m, 线段 PM为n,求m与n的函数关系式.
轴的另一个交点为B,现将抛物线向射线AP方向平移,使P点落在M点处,同时抛物线上的B点落在点D(BD∥PM)处.设抛物线平移前P、B之间的曲线部分与平移后M、D之间的曲线部分,与线段MP、BD所围成的面积为m, 线段 PM为n,求m与n的函数关系式.

【答案】
1.解: (1) 抛物线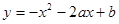 经过点A(1,0)和点P(3,4),
经过点A(1,0)和点P(3,4),
∴ 解得
解得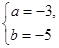 , 抛物线与x轴的交点坐标为(5,0),(1,0),顶点坐标为(3,4)(即P点),
, 抛物线与x轴的交点坐标为(5,0),(1,0),顶点坐标为(3,4)(即P点),
由此可作出抛物线的大致图象如右;
2.)如图,连结PB,MD,
根据平移的性质可知,PB与MD平行且相等,四边形MPBD是平行四边形,
阴影部分的面积就是平行四边形MPBD的面积, 过B点作BE⊥PA,垂足为E,
则有sin∠PAB=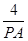 =
=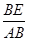 ,
∵A(1,0)和点P(3,4),
,
∵A(1,0)和点P(3,4),
∴PA=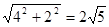 ,而AB=4,
,而AB=4,
∴BE=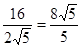 ,
,
∴平行四边形MPBD,其面积为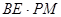 即
即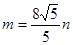 .
.
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (2)若抛物线与
(2)若抛物线与 (2)若抛物线与
(2)若抛物线与 经过点A(1,0)和点P(3,4).
经过点A(1,0)和点P(3,4). 轴的另一个交点为B,现将抛物线向射线AP方向平移,使P点落在M点处,同时抛物线上的B点落在点D(BD∥PM)处.设抛物线平移前P、B之间的曲线部分与平移后M、D之间的曲线部分,与线段MP、BD所围成的面积为m, 线段 PM为n,求m与n的函数关系式.
轴的另一个交点为B,现将抛物线向射线AP方向平移,使P点落在M点处,同时抛物线上的B点落在点D(BD∥PM)处.设抛物线平移前P、B之间的曲线部分与平移后M、D之间的曲线部分,与线段MP、BD所围成的面积为m, 线段 PM为n,求m与n的函数关系式.