题目内容
（2012•遵义）如图，半径为1cm，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为（ ）分析：过点C作CD⊥OB，CE⊥OA，则△AOB是等腰直角三角形，由∠ACO=90°，可知△AOC是等腰直角三角形，由HL定理可知Rt△OCE≌Rt△ACE，故可得出S扇形OEC=S扇形AEC，
与弦OC围成的弓形的面积等于
与弦AC所围成的弓形面积，S阴影=S△AOB即可得出结论．
 |
| OC |
|
| AC |
解答：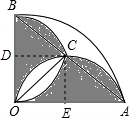
解：过点C作CD⊥OB，CE⊥OA，
∵OB=OA，∠AOB=90°，
∴△AOB是等腰直角三角形，
∵OA是直径，
∴∠ACO=90°，
∴△AOC是等腰直角三角形，
∵CE⊥OA，
∴OE=AE，OC=AC，
在Rt△OCE与Rt△ACE中，
∵
，
∴Rt△OCE≌Rt△ACE，
∵S扇形OEC=S扇形AEC，
∴
与弦OC围成的弓形的面积等于
与弦AC所围成的弓形面积，
同理可得，
与弦OC围成的弓形的面积等于
与弦BC所围成的弓形面积，
∴S阴影=S△AOB=
×1×1=
cm2．
故选C．
解：过点C作CD⊥OB，CE⊥OA，∵OB=OA，∠AOB=90°，
∴△AOB是等腰直角三角形，
∵OA是直径，
∴∠ACO=90°，
∴△AOC是等腰直角三角形，
∵CE⊥OA，
∴OE=AE，OC=AC，
在Rt△OCE与Rt△ACE中，
∵
|
∴Rt△OCE≌Rt△ACE，
∵S扇形OEC=S扇形AEC，
∴
|
| OC |
|
| AC |
同理可得，
|
| OC |
| ||
|
∴S阴影=S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
故选C．
点评：本题考查的是扇形面积的计算与等腰直角三角形的判定与性质，根据题意作出辅助线，构造出直角三角形得出S阴影=S△AOB是解答此题的关键．
练习册系列答案
相关题目
点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．
（2012•遵义）如图，AB是⊙O的弦，AB长为8，P是⊙O上一个动点（不与A、B重合），过点O作OC⊥AP于点C，OD⊥PB于点D，则CD的长为
（2012•遵义）如图，△OAC中，以O为圆心，OA为半径作⊙O，作OB⊥OC交⊙O于B，垂足为O，连接AB交OC于点D，∠CAD=∠CDA．
（2012•遵义）如图，已知抛物线y=ax2+bx+c（a≠0）的图象经过原点O，交x轴于点A，其顶点B的坐标为（3，-