题目内容
 (2012•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点B的坐标为(3,-
(2012•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点B的坐标为(3,-| 3 |
(1)求抛物线的函数解析式及点A的坐标;
(2)在抛物线上求点P,使S△POA=2S△AOB;
(3)在抛物线上是否存在点Q,使△AQO与△AOB相似?如果存在,请求出Q点的坐标;如果不存在,请说明理由.
分析:(1)根据函数经过原点,可得c=0,然后根据函数的对称轴,及函数图象经过点(3,-
)可得出函数解析式,根据二次函数的对称性可直接得出点A的坐标.
(2)根据题意可得点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2
,代入函数解析式可得出点P的横坐标;
(3)分情况讨论,①点Q与点B重合可直接得出点Q的坐标;②点Q不与点B重合,先求出∠BOA的度数,然后可确定∠Q1OA=的度数,继而利用解直角三角形的知识求出x,得出Q1的坐标,利用二次函数图象函数的对称性可得出Q2的坐标.
| 3 |
(2)根据题意可得点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2
| 3 |
(3)分情况讨论,①点Q与点B重合可直接得出点Q的坐标;②点Q不与点B重合,先求出∠BOA的度数,然后可确定∠Q1OA=的度数,继而利用解直角三角形的知识求出x,得出Q1的坐标,利用二次函数图象函数的对称性可得出Q2的坐标.
解答:解:(1)由函数图象经过原点得,函数解析式为y=ax2+bx(a≠0),
又∵函数的顶点坐标为(3,-
),
∴
,
解得:
,
故函数解析式为:y=
x2-
x,
由二次函数图象的对称性可得点A的坐标为(6,0);
(2)∵S△POA=2S△AOB,
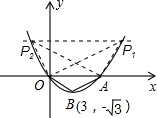
∴点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2
,
代入函数解析式得:2
=
x2-
x,
解得:x1=3+3
,x2=3-3
,
即满足条件的点P有两个,其坐标为:P1(3+3
,2
),P2(3-3
,2
).
(3)存在.
①当点Q与点B重合时,满足△AQO与△AOB相似,
此时点Q的坐标为(3,-
);
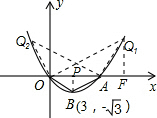
②当点Q与点B不重合时,
过点B作BP⊥OA,则tan∠BOP=
=
,
故可得∠BOA=30°,
设Q1坐标为(x,
x2-
x),过点Q1作Q1F⊥x轴,
∵△OAB∽△OQ1A,
∴∠Q1OA=30°,
故可得OF=
Q1F,即x=
(
x2-
x),
解得:x=9或x=0(舍去),
经检验得此时OA=AQ1,△OQ1A是等腰三角形,且和△OBA相似.
即可得Q1坐标为(9,3
),
根据函数的对称性可得Q2坐标为(-3,3
).
∴在抛物线上存在点Q,使△AQO与△AOB相似,其坐标为:(3,-
)或(9,3
)或(-3,3
).
又∵函数的顶点坐标为(3,-
| 3 |
∴
|
解得:
|
故函数解析式为:y=
| ||
| 9 |
2
| ||
| 3 |
由二次函数图象的对称性可得点A的坐标为(6,0);
(2)∵S△POA=2S△AOB,

∴点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2
| 3 |
代入函数解析式得:2
| 3 |
| ||
| 9 |
2
| ||
| 3 |
解得:x1=3+3
| 3 |
| 3 |
即满足条件的点P有两个,其坐标为:P1(3+3
| 3 |
| 3 |
| 3 |
| 3 |
(3)存在.
①当点Q与点B重合时,满足△AQO与△AOB相似,
此时点Q的坐标为(3,-
| 3 |

②当点Q与点B不重合时,
过点B作BP⊥OA,则tan∠BOP=
| BP |
| OP |
| ||
| 3 |
故可得∠BOA=30°,
设Q1坐标为(x,
| ||
| 9 |
2
| ||
| 3 |
∵△OAB∽△OQ1A,
∴∠Q1OA=30°,
故可得OF=
| 3 |
| 3 |
| ||
| 9 |
2
| ||
| 3 |
解得:x=9或x=0(舍去),
经检验得此时OA=AQ1,△OQ1A是等腰三角形,且和△OBA相似.
即可得Q1坐标为(9,3
| 3 |
根据函数的对称性可得Q2坐标为(-3,3
| 3 |
∴在抛物线上存在点Q,使△AQO与△AOB相似,其坐标为:(3,-
| 3 |
| 3 |
| 3 |
点评:此题属于二次函数的综合题目,涉及了相似三角形的判定与性质,三角形的面积及一元二次方程的解,综合性较强,需要我们仔细分析,分步解答.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目

 点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D. (2012•遵义)如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A、B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为
(2012•遵义)如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A、B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为 (2012•遵义)如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
(2012•遵义)如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.