题目内容
【题目】如图，在平面直角坐标系中，⊙D与y轴相切于点C（0，4），与x轴相交于A、B两点，且AB=6． 
（1）求圆的半径和点D的坐标；
（2）点A的坐标是 ， 点B的坐标是 ， sin∠ACB；
（3）求经过C、A、B三点的抛物线解析式；
（4）设抛物线的顶点为F，证明直线FA与⊙D相切．
【答案】
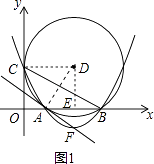
（1）解：过点D作DE⊥AB于E，连接DC、AD，如图1，
则AE=EB= 
AB=3，DC⊥y轴，
∴∠DCO=∠COE=∠DEO=90°，
∴四边形OCDE是矩形，
∴OE=CD，DE=OC=4．
在Rt△ADE中，AD= 
= 
=5，
∴OE=CD=AD=5，
∴圆的半径为5，点D的坐标为（5，4）；
（2）（2，0）；（8，0）；
（3）解：设抛物线的解析式为y=ax2+bx+c，
∵A（2，0），B（8，0），C（0，4）在抛物线y=ax2+bx+c上，
∴ 
，
解得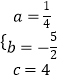 
．
∴抛物线的解析式为y= 
x2﹣ 
x+4；
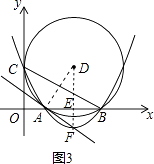
（4）解：连接DA，DF，如图3，
∵D、F都在线段AB的垂直平分线上，
∴DF垂直平分AB．
由y= x2﹣ x+4= （x﹣5）2﹣ 
可得F（5，﹣ ），
∵DF=4+ = 
，AF= 
= 
，
∴DA2+AF2=52+（ ）2= 
=（ ）2=DF2，
∴∠DAF=90°，
∴FA与⊙D相切．
【解析】解：（2）过点D作DE⊥AB于E，连接DB、AD，如图2，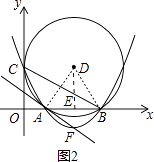 
∵OE=5，AE=EB=3，
∴OA=5﹣3=2，OB=5+3=8．
∵DA=DB，
∴∠ADE=∠BDE= ∠ADB=∠ACB，
∴sin∠ACB=sin∠ADE= 
= ．
故答案分别为：（2，0），（8，0）， ；
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
