题目内容
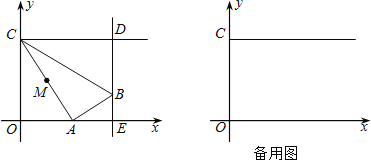
【题目】如图,在平面直角坐标系xOy中,已知直线AB经过点A(﹣2,0),与y轴的正半轴交于点B,且OA=2OB.
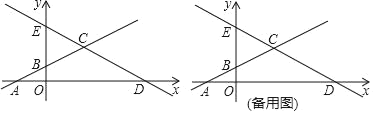
(1)求直线AB的函数表达式;
(2)点C在直线AB上,且BC=AB,点E是y轴上的动点,直线EC交x轴于点D,设点E的坐标为(0,m)(m>2),求点D的坐标(用含m的代数式表示);
(3)在(2)的条件下,若CE:CD=1:2,点F是直线AB上的动点,在直线AC上方的平面内是否存在一点G,使以C,G,F,E为顶点的四边形是菱形?若存在,请求出点G的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x+1;(2)
x+1;(2)![]() ;(3)(2,4)或(﹣2,2)或
;(3)(2,4)或(﹣2,2)或![]()
【解析】
(1)利用待定系数法即可解决问题;
(2)求出点C坐标,利用待定系数法求出直线DE的解析式即可解决问题;
(3)求出点E坐标,分两种情形分别讨论求解即可;
(1)∵A(﹣2,0),OA=2OB,
∴OA=2,OB=1,
∴B(0,1),
设直线AB的解析式为y=kx+b,则有![]()
解得![]()
∴直线AB的解析式为y=![]() x+1.
x+1.
(2)∵BC=AB,A(﹣2,0),B(0,1),
∴C(2,2),
设直线DE的解析式为y=k′x+b′,则有![]()
解得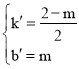
∴直线DE的解析式为![]()
令y=0,得到![]()
∴![]()
(3)如图1中,作CF⊥OD于F.
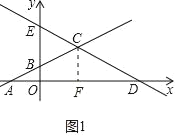
∵CE:CD=1:2,CF∥OE,
∴![]()
∵CF=2,
∴OE=3.
∴m=3.
∴E(0,3),D(6,0),
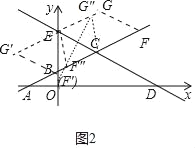
①当EC为菱形ECFG的边时,F(4,3),G(2,4)或F′(0,1),G′(﹣2,2).
②当EC为菱形EF″CG″的对角线时,F″G″垂直平分线段EC,易知直线DE的解析式为![]() ,直线G″F″的解析式为
,直线G″F″的解析式为![]()
由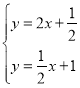 ,解得
,解得![]()
∴F″![]() ,
,
设G″(a,b),则有
∴![]()
∴G″![]()

 特高级教师点拨系列答案
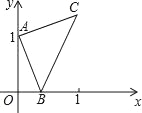
特高级教师点拨系列答案【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤![]() 的解集.
的解集.