��Ŀ����
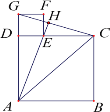
����Ŀ����ͼ�٣��ڳ�����ABCD�У�AB��10 cm��BC��8 cm����P��A��������A��B��C��D·���˶�����Dֹͣ����P���ٶ�Ϊÿ��1 cm��a��ʱ��P���ٶȱ�Ϊÿ��bcm��ͼ���ǵ�P����x�����APD�����S1��cm2����y���룩�ĺ�����ϵͼ��
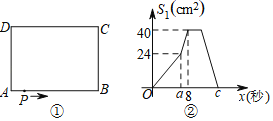
��1������ͼ�����ṩ����Ϣ��a���� ��b���� ��c���� ��
��2����P�������룬��APD�����S1�dz�����ABCD������ķ�֮һ��
���𰸡���1��a��6��b��2��c��17����2����P������5���14.5�룬��APD�����S1�dz�����ABCD������ķ�֮һ.
��������
��1���ɸ��ݺ���ͼ��ֶ����������ε������ʽ�׳��Ըߣ���Ϊ8cmһ��������ʱ��ı仯���仯�����a��b��cΪ����ʱ��ĺͣ�
��2���ɷ������������ɵã���P��AB�е��CD�е�ʱ����APD�����S1�dz�����ABCD������ķ�֮һ��
�⣺��1��������ͼ���֪��
��0��x��aʱ��S1��![]() ��8a��24 ����a��6
��8a��24 ����a��6
��a��x��8ʱ��S1��![]() ��8��[6��1+b��8��6��]��40 ����b��2
��8��[6��1+b��8��6��]��40 ����b��2
��8��x��cʱ��
�ٵ���P��B���˶���C��������APD�����S1��![]() ��8��10��40��cm2��һ��������ʱ���ǣ�8��2��4���룩��
��8��10��40��cm2��һ��������ʱ���ǣ�8��2��4���룩��
�ڵ���P��C���˶���D�㣺����ʱ���ǣ�10��2��5���룩��
����c��8+4+5��17���룩��
�ʴ�Ϊ��a��6��b��2��c��17��
��2���߳�����ABCD����ǣ�10��8��80��cm2��
�൱0��x��aʱ��![]() ��8x��80��
��8x��80��![]() ����x��5��
����x��5��
��12��x��17ʱ��![]() ��8��2��17��x����80��
��8��2��17��x����80��![]() ����x��14.5��
����x��14.5��
���P������5���14��5�룬��APD�����S1�dz�����ABCD������ķ�֮һ��

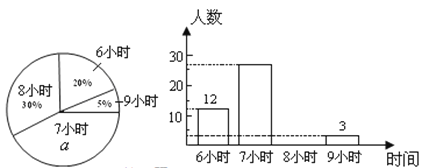
����Ŀ�����������˵ڶ����������۳������Ķ���ȫ���Ķ����Ϊ�˽�����ÿ����Ķ�ʱ������������ȡ�˲���������е��飮���ݵ��������������в�������Ƶ���ֲ�����
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
(1) ��ȫ����
(2) ��ÿ���Ķ�ʱ�䲻���� ![]() �������Ϊ���Ķ�����������������Լ��
�������Ϊ���Ķ�����������������Լ�� ![]() ���ˣ�����������ܳ�Ϊ���Ķ���������������Լ�ж������ˣ�
���ˣ�����������ܳ�Ϊ���Ķ���������������Լ�ж������ˣ�