题目内容
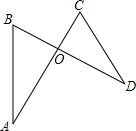（2012•高安市二模）如图，AC与BD相交于点O，在△AOB和△DOC中，已知| OA |
| OD |
| OB |
| OC |
∠AOB=∠DOC
∠AOB=∠DOC
，可证明△AOB∽△DOC．分析：根据相似三角形的判定，两边对应成比例，夹角相等，两三角形相似解答．
解答：解：∵
=
，∠AOB=∠DOC，
∴△AOB∽△DOC（两边对应成比例，夹角相等，两三角形相似）．
故答案为：∠AOB=∠DOC．
| OA |
| OD |
| OB |
| OC |
∴△AOB∽△DOC（两边对应成比例，夹角相等，两三角形相似）．
故答案为：∠AOB=∠DOC．
点评：本题考查了相似三角形的判定，熟记“两边对应成比例，夹角相等，两三角形相似”是解题的关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
（2012•高安市二模）如图，直线AB∥CD，GH与AB、CD分别交于点M、F，若∠GMB=70°，∠CEF=50°，则∠C=