题目内容
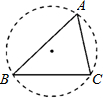（2012•阜新）如图，在△ABC中，BC=3cm，∠BAC=60°，那么△ABC能被半径至少为| 3 |
| 3 |
分析：作圆O的直径CD，连接BD，根据圆周角定理求出∠D=60°，根据锐角三角函数的定义得出sin∠D=
，代入求出CD即可．
| BC |
| CD |
解答：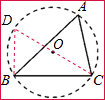
解：作圆O的直径CD，连接BD，
∵弧BC对的圆周角有∠A、∠D，
∴∠D=∠A=60°，
∵直径CD，
∴∠DBC=90°，
∴sin∠D=
，
即sin60°=
，
解得：CD=2
，
∴圆O的半径是
，
故答案为：
．
解：作圆O的直径CD，连接BD，∵弧BC对的圆周角有∠A、∠D，
∴∠D=∠A=60°，
∵直径CD，
∴∠DBC=90°，
∴sin∠D=
| BC |
| CD |
即sin60°=
| 3 |
| CD |
解得：CD=2
| 3 |
∴圆O的半径是
| 3 |
故答案为：
| 3 |
点评：本题考查了圆周角定理，三角形的外接圆与外心，锐角三角函数的定义的应用，关键是得出sin∠D=
，题目比较典型，是一道比较好的题目．
| BC |
| CD |
练习册系列答案
阅读快车系列答案
相关题目
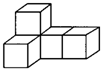（2012•阜新）如图的几何体是由5个完全相同的正方体组成的，这个几何体的左视图是（ ）
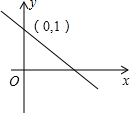（2012•阜新）如图，一次函数y=kx+b的图象与y轴交于点（0，1），则关于x的不等式kx+b＞1的解集是（ ）
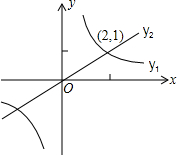（2012•阜新）如图，反比例函数y1=
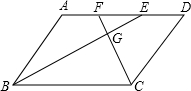（2012•阜新）如图，四边形ABCD是平行四边形，BE平分∠ABC，CF平分∠BCD，BE、CF交于点G．若使EF=
（2012•阜新）如图，一块直角三角板的两个顶点分别在直尺的对边上．若∠1=30°，那么∠2=