题目内容
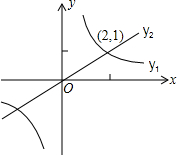（2012•阜新）如图，反比例函数y1=| k1 |
| x |
分析：先根据反比例函数与正比例函数的性质求出B点坐标，由函数图象即可得出结论．
解答：
解：∵反比例函数与正比例函数的图象均关于原点对称，
∴A、B两点关于原点对称，
∵A（2，1），
∴B（-2，-1），
∵由函数图象可知，当0＜x＜2或x＜-2时函数y1的图象在y2的上方，
∴使y1＞y2的x的取值范围是x＜-2或0＜x＜2．
故选D．
解：∵反比例函数与正比例函数的图象均关于原点对称，∴A、B两点关于原点对称，
∵A（2，1），
∴B（-2，-1），
∵由函数图象可知，当0＜x＜2或x＜-2时函数y1的图象在y2的上方，
∴使y1＞y2的x的取值范围是x＜-2或0＜x＜2．
故选D．
点评：本题考查的是反比例函数与一次函数的交点问题，能根据数形结合求出y1＞y2时x的取值范围是解答此题的关键．
练习册系列答案
全能测控一本好卷系列答案
相关题目
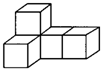（2012•阜新）如图的几何体是由5个完全相同的正方体组成的，这个几何体的左视图是（ ）
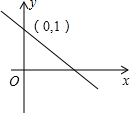（2012•阜新）如图，一次函数y=kx+b的图象与y轴交于点（0，1），则关于x的不等式kx+b＞1的解集是（ ）
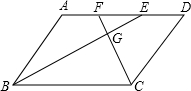（2012•阜新）如图，四边形ABCD是平行四边形，BE平分∠ABC，CF平分∠BCD，BE、CF交于点G．若使EF=
（2012•阜新）如图，一块直角三角板的两个顶点分别在直尺的对边上．若∠1=30°，那么∠2=