题目内容
【题目】如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1 , D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1 , C1的坐标.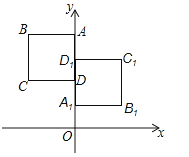
【答案】解:(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1 , D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1 , C1的坐标分别是(2,1),(2,3),
综上,可得
顶点B,C,B1 , C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
【解析】(1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,据此解答即可.
(2)首先根据A,D的坐标分别是(0,4),(0,2),求出正方形ABCD与正方形A1B1C1D1的边长是多少,然后根据A,D1 , D三点的坐标分别是(0,4),(0,3),(0,2),判断出顶点B,C,B1 , C1的坐标各是多少即可.

练习册系列答案
相关题目