题目内容
 如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是
如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是45
45
度.分析:根据折叠的性质和矩形的性质得出∠CBA=∠CBA′,∠CAD=90°,根据角平分线的性质得出∠A′BE=∠DBE,求出∠CBE=∠CBA′+∠A′BE=
∠CAD,代入求出即可.
| 1 |
| 2 |
解答:解:∵将长方形纸片的一角折叠,使顶点A落在点A′处,
∴∠CBA=∠CBA′,∠CAD=90°,
∵BE是∠A′BD的平分线,
∴∠A′BE=∠DBE,
∴∠CBE=∠CBA′+∠A′BE
=
∠ABA′+
∠A′BD
=
(∠ABA′+∠A′BD)
=
∠CAD
=
×90°
=45°,
故答案为:45°.
∴∠CBA=∠CBA′,∠CAD=90°,
∵BE是∠A′BD的平分线,
∴∠A′BE=∠DBE,
∴∠CBE=∠CBA′+∠A′BE
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=45°,
故答案为:45°.
点评:本题考查了矩形的性质,折叠的性质,角平分线定义等知识点,关键是求出∠CBE=
∠CAD.
| 1 |
| 2 |

练习册系列答案
相关题目
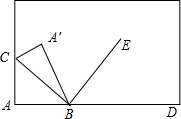 如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的角平分线,求∠CBE的度数,并说明理由.
如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的角平分线,求∠CBE的度数,并说明理由. 5、如图,将长方形纸片的一角折叠,使顶点A落在点A’处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是( )
5、如图,将长方形纸片的一角折叠,使顶点A落在点A’处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是( ) 如图,将长方形纸片的两角分别折叠,使顶点B落在B′处,顶点A落在A′处,EC、ED为折痕,并且点E、A′、B′在同一条直线上.若∠BED=32°,求∠CED和∠AEC的度数.
如图,将长方形纸片的两角分别折叠,使顶点B落在B′处,顶点A落在A′处,EC、ED为折痕,并且点E、A′、B′在同一条直线上.若∠BED=32°,求∠CED和∠AEC的度数. 26、如图,将长方形纸片的两角分别折叠,使顶点B落在B′处,顶点A落在A′处,EC为折痕,点E、A′、B′在同一条直线上.
26、如图,将长方形纸片的两角分别折叠,使顶点B落在B′处,顶点A落在A′处,EC为折痕,点E、A′、B′在同一条直线上.