题目内容
【题目】在△ABC中,AB=15,AC=13,BC边上高AD=12,试求△ABC周长。
【答案】周长为42或32
【解析】本题考查的是勾股定理. 本题应分两种情况进行讨论:(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
解:此题应分两种情况说明: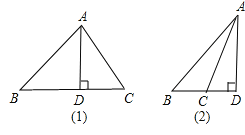
(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD=![]() =
=![]() =9,
=9,
在Rt△ACD中,
CD=![]() =
=![]() =5
=5
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD=![]() =
=![]() =9
=9
在Rt△ACD中,CD=![]() =
=![]() =5
=5
∴BC=9-5=4
∴△ABC的周长为:15+13+4=32
∴当△ABC为锐角三角形时,△ABC的周长为42;
当△ABC为钝角三角形时,△ABC的周长为32.

练习册系列答案
相关题目