题目内容
解方程:
(1)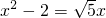
(2) x2-x-1=0(配方法)
x2-x-1=0(配方法)
(1)解:移项得:x2- x-2=0,
x-2=0,
∵b2-4ac=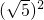 -4×1×(-2)=13,
-4×1×(-2)=13,
∴x= ,
,
即x1= ,x2=
,x2=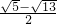 .
.
(2)解:原方程变为:x2-4x-4=0,
移项得:x2-4x=4,
配方得:x2-4x+4=4+4,
(x-2)2=8,
开方得:x-2=±2 ,
,
即x1=2+2 ,x2=2-2
,x2=2-2 .
.
分析:(1)求出b2-4ac的值,代入公式x=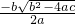 求出即可;
求出即可;
(2)去分母后移项得出x2-4x=4,配方得到(x-2)2=8,开方得出x-2=±2 ,求出方程的解即可.
,求出方程的解即可.
点评:本题考查了解一元二次方程的应用,主要考查学生的计算能力,题目比较典型,难度不大.
 x-2=0,
x-2=0,∵b2-4ac=
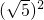 -4×1×(-2)=13,
-4×1×(-2)=13,∴x=
 ,
,即x1=
 ,x2=
,x2=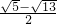 .
.(2)解:原方程变为:x2-4x-4=0,
移项得:x2-4x=4,
配方得:x2-4x+4=4+4,
(x-2)2=8,
开方得:x-2=±2
 ,
,即x1=2+2
 ,x2=2-2
,x2=2-2 .
.分析:(1)求出b2-4ac的值,代入公式x=
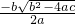 求出即可;
求出即可;(2)去分母后移项得出x2-4x=4,配方得到(x-2)2=8,开方得出x-2=±2
 ,求出方程的解即可.
,求出方程的解即可.点评:本题考查了解一元二次方程的应用,主要考查学生的计算能力,题目比较典型,难度不大.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目