题目内容
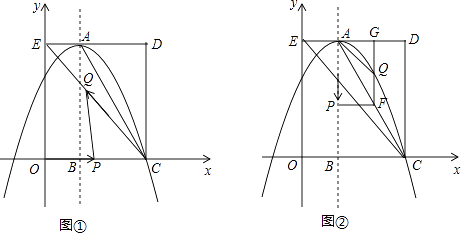
【题目】某公园有一个抛物线形状的观景拱桥ABC，其横截面如图所示，在图中建立的直角坐标系中，抛物线的解析式为y=﹣ 
+c且过顶点C（0，5）（长度单位：m）
（1）直接写出c的值；
（2）现因搞庆典活动，计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯，地毯的价格为20元/m2 ， 求购买地毯需多少元？
（3）在拱桥加固维修时，搭建的“脚手架”为矩形EFGH（H、G分别在抛物线的左右侧上），并铺设斜面EG．已知矩形EFGH的周长为27.5m，求斜面EG的倾斜角∠GEF的度数．（精确到0.1°）
【答案】
（1）解：抛物线的解析式为y=﹣ 
+c，
∵点（0，5）在抛物线上
∴c=5；
（2）解：由（1）知，OC=5，
令y=0，即﹣ +5=0，解得x1=10，x2=﹣10；
∴地毯的总长度为：AB+2OC=20+2×5=30，
∴30×1.5×20=900
答：购买地毯需要900元
（3）解：可设G的坐标为（m，﹣ 
+5）其中m＞0
则EF=2m，GF=﹣ +5，
由已知得：2（EF+GF）=27.5，
即2（2m﹣ +5）=27.5，
解得：m1=5，m2=35（不合题意，舍去），
把m1=5代入，﹣ +5=﹣ 
×52+5=3.75，
∴点G的坐标是（5，3.75），
∴EF=10，GF=3.75，
在Rt△EFG中，tan∠GEF= 
= 
=0.375，
∴∠GEF≈20.6°．
【解析】（1）根据二次函数的实际应用，顶点C（0，5）在抛物线上，直接得到c=5；（2）由（1）知，OC=5，抛物线的值是0，得到一元二次方程﹣x2 +5=0，求出地毯的总长度为AB+2OC=30；（3）根据图像知2（EF+GF）=27.5，得到点G的坐标是（5，3.75），得到EF=10，GF=3.75，在Rt△EFG中，tan∠GEF= GF： EF = ，求出∠GEF≈20.6°；此题是综合题，难度较大，计算和解方程时需认真仔细.
