题目内容
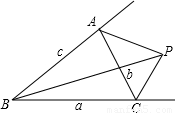
如图,设P为△ABC外一点,P在边AC之外,在∠B之内.S△PBC:S△PCA:S△PAB=4:2:3.又知△ABC三边a,b,c上的高为ha=3,hb=5,hc=6,则P到三边的距离之和为 .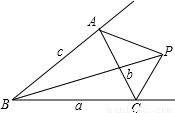
【答案】分析:首先设P到三边的距离为pa,pb,pc,S△PBC=4S,S△PCA=2S,S△PAB=3S,根据同底三角形的面积比等于高的比,即可求得pa,pb,pc的值,则可得到答案.
解答:解:如图设P到三边的距离为pa,pb,pc,S△PBC=4S,S△PCA=2S,S△PAB=3S,
则S△ABC=S△PBC+S△PAB-S△PCA=4S+3S-2S=5S,
∴ ,
,
∴pa= ha=
ha= ,
,
同理可得:pb= ha=2,pc=
ha=2,pc= hc=
hc= ,
,
∴pa+pb+pc= +2+
+2+ =8.
=8.
故答案为:8
点评:此题考查了同底三角形的面积比等于高的比的性质.解题的关键是注意识图,合理应用数形结合思想.
解答:解:如图设P到三边的距离为pa,pb,pc,S△PBC=4S,S△PCA=2S,S△PAB=3S,
则S△ABC=S△PBC+S△PAB-S△PCA=4S+3S-2S=5S,
∴
 ,
,∴pa=
 ha=
ha= ,
,同理可得:pb=
 ha=2,pc=
ha=2,pc= hc=
hc= ,
,∴pa+pb+pc=
 +2+
+2+ =8.
=8.故答案为:8
点评:此题考查了同底三角形的面积比等于高的比的性质.解题的关键是注意识图,合理应用数形结合思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
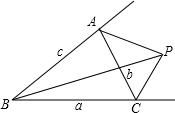 如图,设P为△ABC外一点,P在边AC之外,在∠B之内.S△PBC:S△PCA:S△PAB=4:2:3.又知△ABC三边a,b,c上的高为ha=3,hb=5,hc=6,则P到三边的距离之和为
如图,设P为△ABC外一点,P在边AC之外,在∠B之内.S△PBC:S△PCA:S△PAB=4:2:3.又知△ABC三边a,b,c上的高为ha=3,hb=5,hc=6,则P到三边的距离之和为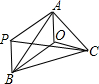 如图,设O为△ABC内一点,且∠AOB=∠BOC=∠COA=120°,P为任意一点(不是O).求证:PA+PB+PC>OA+OB+OC.
如图,设O为△ABC内一点,且∠AOB=∠BOC=∠COA=120°,P为任意一点(不是O).求证:PA+PB+PC>OA+OB+OC.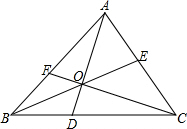 如图,设O为△ABC内一点,连接AO、BO、CO,并延长交BC、CA、AB于点D、E、F,已知S△AOB:S△BOC:S△AOC=3:4:6.则
如图,设O为△ABC内一点,连接AO、BO、CO,并延长交BC、CA、AB于点D、E、F,已知S△AOB:S△BOC:S△AOC=3:4:6.则