Question

【题目】如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠A等于（ ）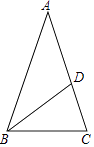
A.30°
B.40°
C.36°
D.45°

Answer 1

【答案】C
【解析】解：∵BD=BC=AD， ∴△ABD，△BCD为等腰三角形，
设∠A=∠ABD=x，则∠C=∠CDB=2x，
又∵AB=AC可知，
∴△ABC为等腰三角形，
∴∠ABC=∠C=2x，
在△ABC中，∠A+∠ABC+∠C=180°，
即x+2x+2x=180°，
解得x=36°，
即∠A=36°．
故选C．
由BD=BC=AD可知，△ABD，△BCD为等腰三角形，设∠A=∠ABD=x，则∠C=∠CDB=2x，又由AB=AC可知，△ABC为等腰三角形，则∠ABC=∠C=2x，在△ABC中，用内角和定理列方程求解．