Question

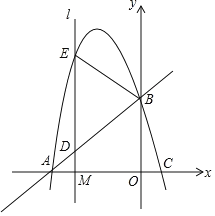
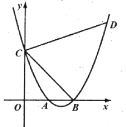
【题目】如图，在平面直角坐标系中，抛物线与轴交于、两点，与轴交于点，点是对称轴右侧抛物线上一点，且，则点的坐标为___________．

Answer 1

【答案】

【解析】

根据已知条件，需要构造直角三角形，过D做DH⊥CR于点H,用含字母的代数式表示出PH、RH,即可求解．

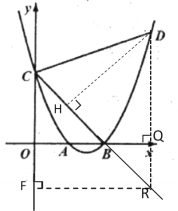
解：过点D作DQ⊥x轴于Q,交CB延长线于R,作DH⊥CR于H,

过R做RF⊥y轴于F,

∵抛物线与轴交于、两点，与轴交于点，

∴A(1,0), B(2,0)C(0,2)

∴直线BC的解析式为y=-x+2

设点D坐标为(m,m-3m+2),R(m,-m+2),

∴DR=m -3m+2-(-m+2)=m -2m

∵OA=OB=2

∴∠CAO=ACO=45°=∠QBR=∠RDH,

∴CR=,

∵

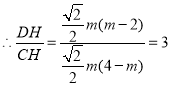
经检验是方程的解.

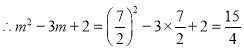
故答案为：