题目内容
【题目】如图,过⊙O外一点P作⊙O的两条切线,切点分别为A、B,点M是劣弧AB上的任一点,过M作⊙0的切线分别交PA、PB于点C、D,过圆心O且垂直于OP的直线与PA、PB分别交于点E、F,那么![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
【答案】A
【解析】连接OA、OB、OC、OD、OM,
∵PA、PB、CD都是⊙O的切线,
∴∠OPE=∠OPF,∠OCA=∠OCD,∠ODM=∠ODB,∠OAC=∠OMC=∠OMD=∠OBD=90°,
∴∠COA=∠COM,∠DOM=∠DOB,
∵PO⊥EF,
∴∠POE=∠POF=90°,
又∵PO=PO,
∴△POE≌△POF
∴∠E=∠F,OE=OF.
∵∠E+∠AOE=90°,∠F+∠FOB=90°,
∴∠AOE=∠FOB,
∵∠AOE+∠AOC+∠COM+∠DOM+∠DOB+∠FOB=180°,
∴2∠FOB+2∠AOC+2∠DOB=180°,
∴∠FOB+∠AOC+∠DOB=90°,
∴∠AOC+∠DOF=90°,
又∵∠AOC+∠ACO=90°,
∴∠ACO=∠DOF,
又∵∠E=∠F,
∴△EOC∽△FDO,
∴EC:FO=EO:FD,
∴EC·FD=FO·EO=EO2=![]() EF2,
EF2,
∴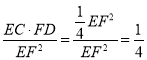 .
.

故选A.

练习册系列答案
相关题目