题目内容
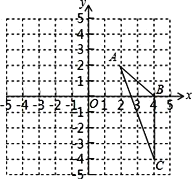
【题目】如图,在平面直角坐标系中,△ABC三个顶点分别是A(2,2),B(4,0),C(4,﹣4)
(1)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2
,得到△A2B2C2,请在y轴右侧画出△A2B2C2
(2)求出∠A2C2B2的正弦值.
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)根据位似图形的定义,分别连接OA、OB、OC,然后分别取它们的中点A2、B2、C2,连接A2B2、A2C2、B2C2,△A2B2C2即为所求;
(2)设CB所在的网格线和点A所在的水平网格线交于点D,可得:AD=2,CD=6,根据勾股定理即可求出AC,然后利用位似图形的性质可得:∠A2C2B2=∠ACB,从而求出:∠A2C2B2的正弦值.
解:(1)根据题意,分别连接OA、OB、OC,然后分别取它们的中点A2、B2、C2,连接A2B2、A2C2、B2C2,此时![]()
∴△A2B2C2即为所求;
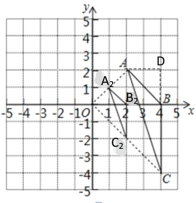
(2)设CB所在的网格线和点A所在的水平网格线交于点D
∴AD=2,CD=6
根据勾股定理可得:AC=![]()
由(1)可知:△ABC和△A2B2C2是位似图形
∴∠A2C2B2=∠ACB
∴sin∠A2C2B2=sin∠ACB=![]()

练习册系列答案
相关题目