题目内容
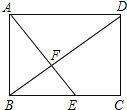
【题目】如图，四边形ABCD是矩形，点E在BC边上，AE与BD交于点F，∠BAE＝∠ADB.
(1)图中与△ABF相似的三角形(不包括△ABF本身)共有_____个.
(2)若BE＝2，AD＝5.求：AB的长.
【答案】(1)5；(2)AB=
.
【解析】
(1)证明AE⊥BD，即可解决问题.
(2)证明△ABD∽△EBA，得到
，而AD＝5，BE＝2，求出AB的长度，即可解决问题.
解：(1)∵四边形ABCD为矩形，
∴∠BAD＝∠ABE＝∠BCD＝90°，而∠BAE＝∠ADB，
∴∠BAF+∠ABF＝∠ABF+∠ADB＝90°，
∴AE⊥BD；
∴△ABE、△BEF、△ABD、△AFD、△BCD均与△ABF相似，
故答案为5.
(2)由(1)知：AE⊥BD，∠ABE＝90°，
∴∠ABF+∠EBF＝∠EBF+∠FEB，
∴∠ABD＝∠AEB，而∠BAD＝∠ABE，
∴△ABD∽△EBA，
∴，而AD＝5，BE＝2，
∴AB＝.
练习册系列答案
相关题目
【题目】某市射击队打算从君君、标标两名运动员中选拔一人参加省射击比赛，射击队对两人的射击技能进行了测评．在相同的条件下，两人各打靶5次，成绩统计如下：
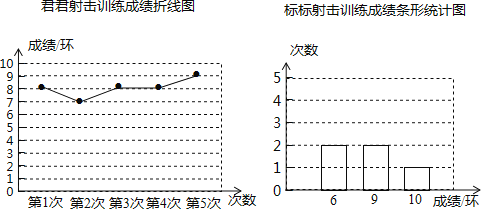
（1）填写下表：
平均数（环） | 中位数（环） | 方差（环2） | |
君君 |
| 8 | 0.4 |
标标 | 8 |
|
|
（2）根据以上信息，若选派一名队员参赛，你认为应选哪名队员，并说明理由．
（3）如果标标再射击1次，命中8环，那么他射击成绩的方差会 ．（填“变大”“变小”或“不变”）
