题目内容
【题目】试解答下列问题:
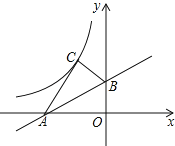
(1)在图1我们称之为“8字形”,请直接写出∠A,∠B,∠C,∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数是 个;
(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系 .
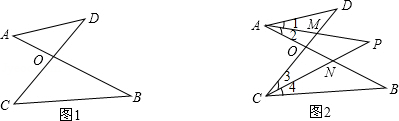
【答案】(1)∠A+∠D=∠C+∠B;(2)6;(3)38°;(4)2∠P=∠D+∠B.
【解析】
试题分析:(1)根据三角形内角和定理即可得出∠A+∠D=∠C+∠B;
(2)根据“8字形”的定义,仔细观察图形即可得出“8字形”共有6个;
(3)先根据“8字形”中的角的规律,可得∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠PAB+∠P②,再根据角平分线的定义,得出∠DAP=∠PAB,∠DCP=∠PCB,将①+②,可得2∠P=∠D+∠B,进而求出∠P的度数;
(4)同(3),根据“8字形”中的角的规律及角平分线的定义,即可得出2∠P=∠D+∠B.
解:(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
故答案为:∠A+∠D=∠C+∠B;
(2)①线段AB、CD相交于点O,形成“8字形”;
②线段AN、CM相交于点O,形成“8字形”;
③线段AB、CP相交于点N,形成“8字形”;
④线段AB、CM相交于点O,形成“8字形”;
⑤线段AP、CD相交于点M,形成“8字形”;
⑥线段AN、CD相交于点O,形成“8字形”;
故“8字形”共有6个;
故答案为:6;
(3)∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠PAB+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:
∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B,
又∵∠D=40度,∠B=36度,
∴2∠P=40°+36°,
∴∠P=38°;
(4)关系:2∠P=∠D+∠B.
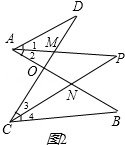
由∠D+∠1+∠2=∠B+∠3+∠4①
由∠ONC=∠B+∠4=∠P+∠2,②
①+②得:
∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1,
∠D+2∠B=2∠P+∠B,
即2∠P=∠D+∠B.
故答案为:2∠P=∠D+∠B.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案