题目内容
【题目】如图1,在平面直角坐标系中,抛物线y=ax2﹣4ax﹣6(a>0)与x轴交于A,B两点,且OB=3OA,与y轴交于点C,抛物线的顶点为D,对称轴与x轴交于点E.
(1)求该抛物线的解析式,并直接写出顶点D的坐标;
(2)如图2,直线y=![]() +n与抛物线交于G,H两点,直线AH,AG分别交y轴负半轴于M,N两点,求OM+ON的值;
+n与抛物线交于G,H两点,直线AH,AG分别交y轴负半轴于M,N两点,求OM+ON的值;
(3)如图1,点P在线段DE上,作等腰△BPQ,使得PB=PQ,且点Q落在直线CD上,若满足条件的点Q有且只有一个,求点P的坐标.
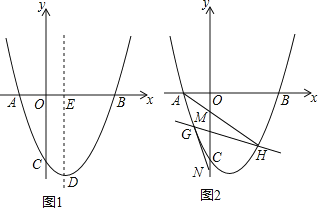
【答案】(1)y=![]() (x﹣2)2﹣8,D(2,﹣8)(2)9;(3)P(2,8﹣4
(x﹣2)2﹣8,D(2,﹣8)(2)9;(3)P(2,8﹣4![]() )
)
【解析】
(1)由OB=3OA可设A(-t,0),B(3t,0),代入抛物线解析式即得到关于a、t的二元方程,解方程求出a即求得抛物线解析式,配方即得到顶点D的坐标.
(2)由(1)求得t=2可知点A(-2,0),设G(x1,![]() x12-2x1-6),H(x2,
x12-2x1-6),H(x2,![]() x22-2x2-6),把直线y=
x22-2x2-6),把直线y=![]() x+n与抛物线解析式联立方程组,消去y后整理得关于x的一元二次方程,x1、x2即为方程的解,根据韦达定理求得x1+x2=3.设直线AG解析式为y=kx+b,把点A、G坐标代入求出b的值即为点N纵坐标,进而得到用x1表示的ON的值,同理可求得用x2表示的OM的值,相加再把x1+x2代入即求得OM+ON的值.
x+n与抛物线解析式联立方程组,消去y后整理得关于x的一元二次方程,x1、x2即为方程的解,根据韦达定理求得x1+x2=3.设直线AG解析式为y=kx+b,把点A、G坐标代入求出b的值即为点N纵坐标,进而得到用x1表示的ON的值,同理可求得用x2表示的OM的值,相加再把x1+x2代入即求得OM+ON的值.
(3)以点P为圆心,PB长为半径的⊙P,由于满足PB=PQ(即点Q在⊙P上)且点Q在直线CD上的点Q有且只有一个,即⊙P与直线CD只有一个公共点,所以直线CD与⊙P相切于点Q.由(1)得点C、D坐标可知直线CD与DE夹角为45°,△PDQ为等腰直角三角形,PD=
2 |
PQ=
2 |
PB.设点P纵坐标为p,用p表示PB和PD的长并列得方程即可求p的值.由于点P在线段DE上,故p的值为负数,舍去正数解.
(1)∵抛物线y=ax2﹣4ax﹣6与x轴交于A,B两点,OB=3OA
∴设A(﹣t,0),B(3t,0)(t>0)
∴ 解得:
解得:![]()
∴抛物线解析式为y=![]() x2﹣2x﹣6=
x2﹣2x﹣6=![]() (x﹣2)2﹣8
(x﹣2)2﹣8
∴顶点D的坐标为(2,﹣8)
(2)∵t=2
∴A(﹣2,0)
设抛物线上的点G(x1,![]() x12﹣2x1﹣6),H(x2,
x12﹣2x1﹣6),H(x2,![]() x22﹣2x2﹣6)
x22﹣2x2﹣6)
∵直线y=![]() +n与抛物线交于G,H两点
+n与抛物线交于G,H两点
∴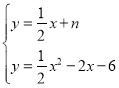 整理得:x2﹣3x﹣12﹣2n=0
整理得:x2﹣3x﹣12﹣2n=0
∴x1+x2=3
设直线AG解析式为y=kx+b,即N(0,b)(b<0)
∴
①×x1得:﹣2kx1+bx1=0 ③
②×2得:2kx1+2b=x12﹣4x1﹣12 ④
③+④得:(x1+2)b=(x1+2)(x1﹣6)
∵点G与A不重合,即x1+2≠0
∴b=x1﹣6即ON=﹣b=6﹣x1
同理可得:OM=6﹣x2
∴OM+ON=6﹣x2+6﹣x1=12﹣(x1+x2)=12﹣3=9
(3)如图,过点C作CF⊥DE于点F,以点P为圆心、PB为半径作圆

∵PB=PQ
∴点Q在⊙P上
∵有且只有一个点Q在⊙P上又在直线CD上
∴⊙P与直线CD相切于点Q
∴PQ⊥CD
由(1)得:B(6,0),C(0,﹣6),D(2,﹣8)
∴CF=2,DF=﹣6﹣(﹣8)=2,即CF=DF
∴∠CDF=45°
∴△DPQ为等腰直角三角形
∴PD=![]() PQ
PQ
∴PD2=2PQ2=2PB2
设P(2,p)(﹣8≤p≤0)
∴PD=p+8,PB2=(6﹣2)2+p2=16+p2
∴(p+8)2=16+p2
解得:p1=8﹣4![]() ,p2=8+4
,p2=8+4![]() (舍去)
(舍去)
∴点P坐标为(2,8﹣4![]() )
)