题目内容
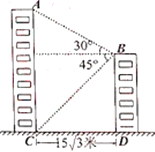
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 右侧),点
右侧),点![]() 为抛物线的顶点.点
为抛物线的顶点.点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,点
,点![]() 恰好旋转到点
恰好旋转到点![]() ,连接
,连接![]() .
.


(1)求点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)如图2,过顶点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作
作![]() 轴,点
轴,点![]() 为垂足,使得
为垂足,使得![]() 与
与![]() 相似(不含全等).
相似(不含全等).
①求出一个满足以上条件的点![]() 的横坐标;
的横坐标;
②直接回答这样的点![]() 共有几个?
共有几个?
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)证明见解析;(3)①点P的横坐标为
;(2)证明见解析;(3)①点P的横坐标为![]() ,
,![]() ,
,![]() ,②点P共有3个.
,②点P共有3个.
【解析】
(1)令y=0,可得关于x的方程,解方程求得x的值即可求得A、B两点的坐标,对解析式配方可得顶点D的坐标;
(2)由![]() ,CO⊥AF,可得OF=OA=1,如图2,易得
,CO⊥AF,可得OF=OA=1,如图2,易得![]() ,由此可得
,由此可得![]() ,继而证明
,继而证明![]() 为等边三角形,推导可得
为等边三角形,推导可得![]() ,再由
,再由![]() ,
,![]() ,可得
,可得![]() ,问题得证;
,问题得证;
(3)①设点![]() 的坐标为
的坐标为 ,分三种情况:点
,分三种情况:点![]() 在
在![]() 点左侧,点
点左侧,点![]() 在
在![]() 点右侧,点
点右侧,点![]() 在
在![]() 之间,分别讨论即可得;
之间,分别讨论即可得;
②由①的结果即可得.
(1)令![]() ,
,
解得![]() 或
或![]() ,
,
故![]() ,
,![]() ,
,
配方得![]() ,故
,故![]() ;
;
(2)∵![]() ,CO⊥AF,
,CO⊥AF,
∴OF=OA=1,
如图,DD1⊥轴,∴DD1//CO,

∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴CF=![]() =2,
=2,
∴![]() ,
,
即![]() 为等边三角形,
为等边三角形,
∴∠AFC=∠ACF=60°,
∵∠ECF=∠ACF,
∴![]() ,
,
∴![]() ,
,
∵CF:DF=OF:FD1=1:2,
∴DF=4,∴CD=6,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
(3)①设点![]() 的坐标为
的坐标为 ,
,
(ⅰ)当点![]() 在
在![]() 点左侧时,
点左侧时,

因为![]() 与
与![]() 相似,
相似,
则1)![]() ,
,
即 ,
,
∴![]() (舍),x2=-11;
(舍),x2=-11;
2)![]() ,
,
即 ,
,
∴![]() (舍),
(舍),![]() ;
;
(ⅱ)当点![]() 在
在![]() 点右侧时,
点右侧时,

因为![]() 与
与![]() 相似,
相似,
则3)![]() ,
,
即 ,
,
∴![]() (舍),
(舍),![]() (舍);
(舍);
4)![]() ,
,
即 ,
,
∴![]() (舍),
(舍),![]() (舍);
(舍);
(ⅲ)当点![]() 在
在![]() 之间时,
之间时,

∵![]() 与
与![]() 相似,
相似,
则5)![]() ,
,
即 ,
,
∴![]() (舍),
(舍),![]() (舍);
(舍);
6)![]() ,
,
即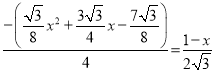 ,
,
∴![]() (舍),
(舍),![]() ;
;
综上所述,点![]() 的横坐标为
的横坐标为![]() ,
,![]() ,
,![]() ;
;
②由①可得这样的点P共有3个.

【题目】甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
施工时间/天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
累计完成施工量/米 | 35 | 70 | 105 | 140 | 160 | 215 | 270 | 325 | 380 |
下列说法错误的是( )
A. 甲队每天修路20米
B. 乙队第一天修路15米
C. 乙队技术改进后每天修路35米
D. 前七天甲,乙两队修路长度相等
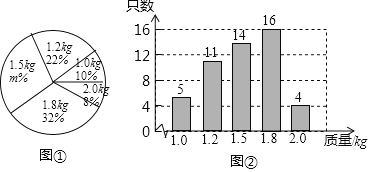
【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:无论![]() 为任何实数,此方程总有两个实数根;
为任何实数,此方程总有两个实数根;
(2)若方程的两个实数根为![]() 、
、![]() ,满足
,满足![]() ,求
,求![]() 的值;
的值;
(3)若![]() △
△![]() 的斜边为5,另外两条边的长恰好是方程的两个根
的斜边为5,另外两条边的长恰好是方程的两个根![]() 、
、![]() ,求
,求![]()
![]() 的内切圆半径.
的内切圆半径.
【题目】某中学抽取了40名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
组别 | 时间/小时 | 频数/人数 |
A组 |
| 2 |
B组 |
| m |
C组 |
| 10 |
D组 |
| 12 |
E组 |
| 7 |
F组 |
| 4 |
频数分布表
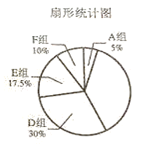
请根据图表中的信息解答下列问题:
(1)求频数分布表中m的值;
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全扇形统计图;
(3)已知F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从F组中随机选取2名学生,恰好都是女生。