题目内容
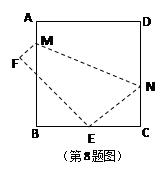
如图，将边长为8㎝的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在F处，折痕为MN，则线段CN的长是（ ）
| A．3cm | B．4cm | C．5cm | D．6cm |
A
分析：根据折叠的性质，只要求出DN就可以求出NE，在直角△CEN中，若设CN=x，则DN=NE=8-x，CE=4cm，根据勾股定理就可以列出方程，从而解出CN的长．
解答：解：设CN=xcm，则DN=（8-x）cm，由折叠的性质知EN=DN=（8-x）cm，
而EC=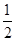
BC=4cm，在Rt△ECN中，由勾股定理可知EN2=EC2+CN2，即（8-x）2=16+x2，
整理得16x=48，所以x=3．
故选A．
解答：解：设CN=xcm，则DN=（8-x）cm，由折叠的性质知EN=DN=（8-x）cm，
而EC=
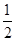BC=4cm，在Rt△ECN中，由勾股定理可知EN2=EC2+CN2，即（8-x）2=16+x2，整理得16x=48，所以x=3．
故选A．
练习册系列答案
相关题目
绕点
按顺时针方向旋转到
的位置，其中
交直线
于点
，
分别交直线
于点
，则旋转后的图中，全等三角形共有（ ）
的方格纸中将图（1）中的图形N平移后的位置如图（2）中所示，那么正确的平移方法是先向 移动 格，再向 移动 格
