题目内容
【题目】已知反比例函数![]() (k≠8)的图像经过点A(1,6).
(k≠8)的图像经过点A(1,6).
(1)求k的值;
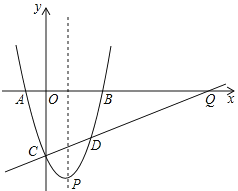
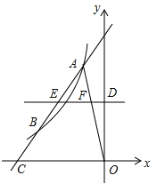
(2)如图,过点A作直线AC与函数![]() 的图像交于点B,与x轴交于点C,且AB=2BC,求直线AC的解析式;
的图像交于点B,与x轴交于点C,且AB=2BC,求直线AC的解析式;
(3)在(2)的条件下,连接OA,过y轴的正半轴上的一点D作直线DE∥x轴,分别交线段AC、OA于点E、F,若△AEF的面积为![]() ,求点D的坐标.
,求点D的坐标.
【答案】(1)2;(2)![]() ;(3)D(0,4).
;(3)D(0,4).
【解析】
(1)根据点![]() 的坐标,利用待定系数法即可求出
的坐标,利用待定系数法即可求出![]() 的值;
的值;
(2)根据![]() 结合点
结合点![]() 、
、![]() 的纵坐标即可得出点
的纵坐标即可得出点![]() 的纵坐标,利用反比例函数图象上点的坐标特征即可求出点
的纵坐标,利用反比例函数图象上点的坐标特征即可求出点![]() 的坐标,根据点
的坐标,根据点![]() 、
、![]() 的坐标利用待定系数法即可求出直线
的坐标利用待定系数法即可求出直线![]() 的解析式,即为直线AC的解析式;
的解析式,即为直线AC的解析式;
(3)先求出△ACO的面积,由DE∥x轴可知![]() ,由面积比等于相似比的平方可求出
,由面积比等于相似比的平方可求出![]() ,由此求出E点纵坐标,即可得D点坐标.
,由此求出E点纵坐标,即可得D点坐标.
解:(1)将点![]() 代入
代入![]() 中,
中,
得:![]() ,解得:
,解得:![]() .
.
(2)![]() ,点
,点![]() 的纵坐标为6,点
的纵坐标为6,点![]() 的纵坐标为0,
的纵坐标为0,
![]() 点
点![]() 的纵坐标为2,
的纵坐标为2,
![]() 点
点![]() 为反比例函数
为反比例函数![]() 上的图象,
上的图象,
![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 、
、![]() 代入
代入![]() 中,
中,
得:![]() ,解得:
,解得:![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
(3)令![]() 中
中![]() ,则
,则![]() ,
,
![]() .
.
∴![]() ,
,
∵DE∥x轴,
∴![]() ,
,
∴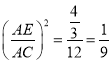 ,
,
∴![]() ,
,
∴点![]() 的纵坐标为4,
的纵坐标为4,
∴点D的坐标![]() .
.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】为了了解某区九年级数学教学质量检测情况,进行了抽样调查,其过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:随机抽取甲、乙两所学校中各自取20名学生的数学成绩进行分析
甲:91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙:84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理数据:表一
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 | 0 | 0 | 1 | 2 | 8 | 5 |
分析数据:表二
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | 115.25 |
得出结论:
(1)若甲学校有400名九年级学生,估计这次考试成绩80分(包含80分)以上人数为 .
(2)可以推断出 (填:甲或乙)学校学生的数学水平较高,理由是 (至少从两个不同角度说明推断的合理性).
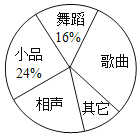
【题目】某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:
最喜爱的节目 | 人数 |
歌曲 | 15 |
舞蹈 | a |
小品 | 12 |
相声 | 10 |
其它 | b |
(1)在此次调查中,该校一共调查了 名学生;
(2)a= ;b= ;
(3)在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;
(4)若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.