题目内容
【题目】规定:若y表示一个函数,令M=|y|,我们则称函数M为函数y的“幸福函数”.
(1)请写出一次函数y=x﹣3的“幸福函数”M的解析式(解析式中不能含有绝对值);
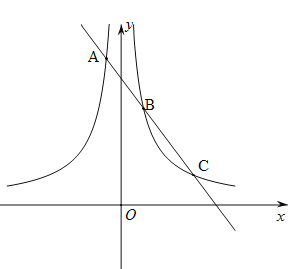
(2)若一次函数y=![]() 与反比例函数y=
与反比例函数y=![]() (k>0)的“幸福函数”M有三个交点,从左至右依次为A,B,C三点,并且BC=
(k>0)的“幸福函数”M有三个交点,从左至右依次为A,B,C三点,并且BC=![]() ,求点A的坐标;
,求点A的坐标;
(3)已知a、b为实数,二次函数y=x2+ax+b的“幸福函数”M,M=2恒有三个不等的实数根.
①求b的最小值;
②若该方程的三个不等实根恰为一直角三角形的三条边,求a和b的值.
【答案】(1) M=![]() ;(2) A(﹣1,8);(3) ①-2;②a=﹣16,b=62.
;(2) A(﹣1,8);(3) ①-2;②a=﹣16,b=62.
【解析】
(1)根据“幸福函数”求解即可;
(2)由题意设B(m,﹣![]() m+
m+![]() ),C(n,﹣
),C(n,﹣![]() n+
n+![]() ),且m<n,由BC=
),且m<n,由BC=![]() ,得到
,得到![]() ,解得n=m+1,则C(m+1,﹣
,解得n=m+1,则C(m+1,﹣![]() m+
m+![]() ﹣
﹣![]() ),由B、C都在反比例函数y=
),由B、C都在反比例函数y=![]() 上,可得m(﹣
上,可得m(﹣![]() m+
m+![]() )=(m+1)(﹣
)=(m+1)(﹣![]() m+
m+![]() ),解得:m=2,B(2,4),把B(2,4)代入y=
),解得:m=2,B(2,4),把B(2,4)代入y=![]() 得到k=8,解方程组
得到k=8,解方程组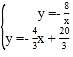 可得的A坐标;
可得的A坐标;
(3)①由题意:抛物线y=x2+ax+b的顶点坐标的纵坐标为﹣2,由此构建二次函数,利用二次函数的性质即可解决问题;
②当y=2时,2=x2+ax+b,可得x2+ax+b﹣2=0,设方程的两个根为x1,x2,(x1<x2),则x1+x2=﹣a,x1x2=b﹣2,由方程M=2的三个不等实根恰为一直角三角形的三条边,则有:x22=x12+(﹣![]() )2,构建方程组求出a、b即可.
)2,构建方程组求出a、b即可.
(1)M=![]() .
.
(2)由题意设B(m,﹣![]() m+
m+![]() ),C(n,﹣
),C(n,﹣![]() n+
n+![]() ),且m<n.
),且m<n.
∵BC=![]() ,∴
,∴![]() ,解得:n=m+1,则C(m+1,﹣
,解得:n=m+1,则C(m+1,﹣![]() m+
m+![]() ﹣
﹣![]() ).
).
∵B、C都在反比例函数y=![]() 上,∴m(﹣
上,∴m(﹣![]() m+
m+![]() )=(m+1)(﹣
)=(m+1)(﹣![]() m+
m+![]() ),解得:m=2,∴B(2,4),把B(2,4)代入y=
),解得:m=2,∴B(2,4),把B(2,4)代入y=![]() 得到k=8,由
得到k=8,由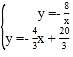 ,解得:
,解得:![]() 或
或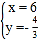 ,∴A(﹣1,8).
,∴A(﹣1,8).
(3)①由题意:抛物线y=x2+ax+b的顶点坐标的纵坐标为﹣2,∴﹣2=![]() ,∴b=
,∴b=![]() a2﹣2.
a2﹣2.
∵![]() >0,∴b有最小值,最小值为﹣2.
>0,∴b有最小值,最小值为﹣2.
②当y=2时,2=x2+ax+b,∴x2+ax+b﹣2=0,设方程的两个根为x1,x2,(x1<x2),则x1+x2=﹣a,x1x2=b﹣2.
∵方程M=2的三个不等实根恰为一直角三角形的三条边,则有:x22=x12+(﹣![]() )2,∴(x2+x1)(x2﹣x1)=
)2,∴(x2+x1)(x2﹣x1)=![]() ,∴x2﹣x1=﹣
,∴x2﹣x1=﹣![]() ,∴(x1+x2)2﹣4x1x2=
,∴(x1+x2)2﹣4x1x2=![]() a2,∴a2﹣4(b﹣2)=
a2,∴a2﹣4(b﹣2)=![]() a2①
a2①
b=![]() a2﹣2②
a2﹣2②
由①②可得:b=62,a=±16.
∵x1+x2=﹣a>0,∴a<0,∴a=﹣16.