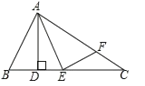
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() 点.
点.

(1)如图①,若![]() 于
于![]() 点,
点,![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,若![]() 交
交![]() 于
于![]() 点,求证:
点,求证:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)首先计算出∠B,∠BAC的度数,然后可得∠EAC=30°,再根据直角三角形两锐角互余可得∠DAC的度数,进而可得答案;
(2)首先证明∠DAE=∠FEC,然后再根据三角形内角和定理可得∠EAC=90°![]() ∠C,再利用角之间的和差关系可得∠DAE=∠DAC∠EAC,利用等量代换可得∠DAE=
∠C,再利用角之间的和差关系可得∠DAE=∠DAC∠EAC,利用等量代换可得∠DAE=![]() ∠C,进而可得结论.
∠C,进而可得结论.
(1)解:∵∠C=40°,∠B=2∠C,
∴∠B=80°,
∴∠BAC=60°,
∵AE平分∠BAC,
∴∠EAC=30°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=50°,
∴∠DAE=50°30°=20°;
(2)证明:作AD⊥BC 于D点,如图,∵EF⊥AE,
∴∠AEF=90°,
∴∠AED+∠FEC=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠FEC,
∵AE平分∠BAC,
∴∠EAC=![]() ∠BAC=
∠BAC=![]() (180°∠B∠C)=
(180°∠B∠C)=![]() (180°3∠C)=90°
(180°3∠C)=90°![]() ∠C,
∠C,
∵∠DAE=∠DAC∠EAC,
∴∠DAE=∠DAC(90°![]() ∠C)=90°∠C90°+
∠C)=90°∠C90°+![]() ∠C=
∠C=![]() ∠C,
∠C,
∴∠FEC=![]() ∠C,
∠C,
∴∠C=2∠FEC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





