题目内容
【题目】如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
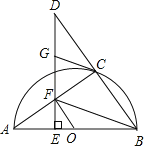
(1)求证:CG是⊙O的切线;
(2)若△AFB的面积是△DCG的面积的2倍,求证:OF∥BC.
【答案】见解析
【解析】
试题分析:(1)连接OC.欲证CG是⊙O的切线,只需证明∠CGO=90°,即CG⊥OC;
(2)根据直角三角形ABC、直角三角形DCF的面积公式,以及直角三角形斜边的中线等于斜边的一半求得AC=2AF;然后根据三角形中位线的判定与定理证得该结论.
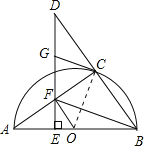
证明:(1)如图,连接OC.
在△ABC中,∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角);
又∵OA=OC,
∴∠A=∠ACO(等边对等角);
在Rt△DCF中,∵点G为DF的中点,∴CG=GF(直角三角形斜边上的中线是斜边的一半),
∴∠GCF=∠CFG(等边对等角);
∵DE⊥AB(已知),∠CFG=∠AFE(对顶角相等);
∴在Rt△AEF中,∠A+∠AFE=90°;
∴∠ACO+∠GCF=90°,即∠GCO=90°,
∴CG⊥OC,
∴CG是⊙O的切线;
(2)∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),即AC⊥BD;
又∵CD=BC,点G为DF的中点,
∴S△AFB=S△ABC﹣S△BCF=![]() (ACBC﹣CFBC),S△DCG=
(ACBC﹣CFBC),S△DCG=![]() S△FCD=
S△FCD=![]() ×
×![]() DCCF=
DCCF=![]() BCCF;
BCCF;
∵△AFB的面积是△DCG的面积的2倍,
∴![]() (ACBC﹣CFBC)=2×
(ACBC﹣CFBC)=2×![]() BCCF,
BCCF,
∴AC=2CF,即点F是AC的中点;
∵O点是AB的中点,
∴OF是△ABC的中位线,
∴OF∥BC.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目