题目内容
【题目】如图，在Rt△ABC中，∠ACB = 90°，BC = 3，AC = 4，点D为边AB上一点．将△BCD沿直线CD翻折，点B落在点E处，联结AE．如果AE // CD，那么BE =________．
【答案】
（或4.8）
【解析】
过D作DG⊥BC于G，依据折叠的性质即可得到CD垂直平分BE，再根据AE∥CD，得出CD＝BD＝2.5，进而得到BG＝1.5，再根据
BC×DG＝CD×BF，即可得到BF的长，即可得出BE的长．
解：如图所示，过D作DG⊥BC于G，
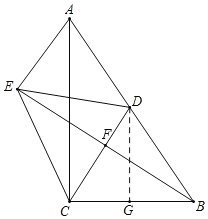
由折叠可得，CD垂直平分BE，
∴当CD∥AE时，∠AEB＝∠DFB＝90°，
∴∠DEB+∠DEA＝90°，∠DBE+∠DAE＝90°，
∵DB＝DE，
∴∠DEB＝∠DBE，
∴∠DAE＝∠DEA，
∴AD＝DE，
∴AD＝BD，
∴D是AB的中点，
∴Rt△ABC中，CD＝BD＝2.5，
∵DG⊥BC，
∴BG＝1.5，
∴Rt△BDG中，DG＝2，
∵BC×DG＝CD×BF，
∴BF＝
＝
，
∴BE＝2BF＝
，
故答案为．
【题目】《中国诗词大会》以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨，力求通过对诗词知识的比拼及赏析，带动全民重温那些曾经学过的古诗词，分享诗词之美，感受诗词之趣，从古人的智慧和情怀中汲取营养，涵养心灵，自开播以来深受广大师生的喜爱．某学校为了提高学生的诗词水平，倡导全校3000名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛．为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根据调查结果绘制成的条形和扇形统计图如图所示．
（整理、描述数据）：
大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”：
一周诗词背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 16 | 24 | 32 | 78 |
| 35 |
（分析数据）：
平均数 | 中位数 | 众数 | |
大赛之前 | 5 |
|
|
大赛之后 | 6 | 6 | 6 |
请根据调查的信息
（1）补全条形统计图；
（2）计算
首，
首，
首，并估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数；
（3）根据调査的相关数据，选择适当的统计量评价该校经典诗词诵背系列活动的效果．
【题目】某学校在A、B两个校区各有九年级学生200人，为了解这两个校区九年级学生的教学学业水平的情况，进行了抽样调查，过程如下，请补充完整．
收集数据：从A、B两个校区各随机抽取20名学生，进行了数学学业水平测试，测试成绩（百分制）如下：
A校区 86 74 78 81 76 75 86 70 75 90
75 79 81 70 74 80 87 69 83 77
B校区 80 73 70 82 71 82 83 93 77 80
81 93 81 73 88 79 81 70 40 83
整理、描述数据 按如下分数段整理、描述这两组样本数据：
成绩x 人数 校区 | 40≤x＜50 | 50≤x＜60 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x≤100 |
A | 0 | 0 | 1 | 11 | 7 | 1 |
B |
（说明：成绩80分及以上的学业水平优秀，70﹣79分为淡定业水平良好，60﹣69分为学业水平合格，60分以下为学业水平不合格）
分析数据 两组样本数据的平均数、中位数、众数如下表所示：
校区 | 平均数 | 中位数 | 众数 |
A | 78.3 | m | 75 |
B | 78 | 80.5 | 81 |
其中m＝ ；
得出结论：a．估计B校区九年级数学学业水平在优秀以上的学生人数为 ；
b．可以推断出 校区的九年级学生的数学学业水平较高，理由为 （至少从两个不同的角度说明推断的合理性）．
