题目内容
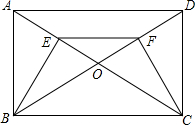 如图,E、F分别是矩形ABCD的对角线以AC、BD上两点,且AE=DF.
如图,E、F分别是矩形ABCD的对角线以AC、BD上两点,且AE=DF.求证:(1)△BOE≌△COF;(2)四边形BCFE是等腰梯形.
分析:本题可以根据全等三角形的判定定理、矩形的性质来证明(1).根据梯形的判定定理一组对边相互平行,另一组对边不平行的为梯形,由等腰梯形的性质两腰相等为等腰梯形可以证明(2).
解答:证明:(1)矩形ABCD的对角线AC、BD相交于O,
∴OB=OC,OA=OD,
又∵AE=DF,
∴OE=OF,
在△BOE和△COF中,
,
∴△BOE≌△COF(SAS);
(2)在等腰△EOF中,∠OEF=
,
在等腰△AOD中,∠OAD=
,
∴∠OEF=∠OAD,
又∵∠OCB=∠OAD,
∴∠OEF=∠OCB,
∴EF∥BC.
又由题意知,EF≠BC,
∴四边形BCFE是梯形.
由(1)△BOE≌△COF,
∴BE=CF,
∴四边形BCFE是等腰梯形.
∴OB=OC,OA=OD,
又∵AE=DF,
∴OE=OF,
在△BOE和△COF中,
|
∴△BOE≌△COF(SAS);
(2)在等腰△EOF中,∠OEF=
| 180°-∠EOF |
| 2 |
在等腰△AOD中,∠OAD=
| 180°-∠EOF |
| 2 |
∴∠OEF=∠OAD,
又∵∠OCB=∠OAD,
∴∠OEF=∠OCB,
∴EF∥BC.
又由题意知,EF≠BC,
∴四边形BCFE是梯形.
由(1)△BOE≌△COF,
∴BE=CF,
∴四边形BCFE是等腰梯形.
点评:解决本题的关键是读懂图意,得到相应的四边形的各边之间的关系.熟练掌握三角形以及梯形的性质.

练习册系列答案
相关题目

 ,直线y=
,直线y=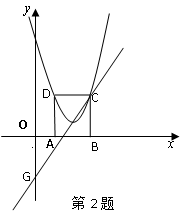
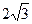 ,直线y=
,直线y= 经过点C,交y轴于点G
经过点C,交y轴于点G
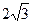 ,直线y=
,直线y=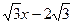 经过点C,交y轴于点G
经过点C,交y轴于点G
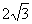 ,直线y=
,直线y= 经过点C,交y轴于点G
经过点C,交y轴于点G