题目内容
【题目】如图,在△BC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.若使四边形ADCF是正方形,则应在△ABC中再添加一个条件为_____.
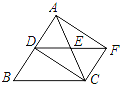
【答案】∠ACB=90°
【解析】
先证明四边形ADCF是平行四边形,再证明AC=DF即可,再利用∠ACB=90°得出答案即可.
∠ACB=90°时,四边形ADCF是正方形,
理由:∵E是AC中点,
∴AE=EC,
∵DE=EF,
∴四边形ADCF是平行四边形,
∵AD=DB,AE=EC,
∴DE=![]() BC,
BC,
∴DF=BC,
∵CA=CB,
∴AC=DF,
∴四边形ADCF是矩形,
点D、E分别是边AB、AC的中点,
∴DE∥BC,
∵∠ACB=90°,
∴∠AED=90°,
∴矩形ADCF是正方形.
故答案为:∠ACB=90°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?