题目内容
【题目】如图,在平行四边形中,点O为对角线BD的中点,DE、BF分别平分∠ADC和∠ABC.
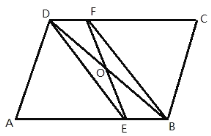
(1)求证:EF、BD互相平分;
(2)若∠A=60,AE=2EB,AD=4,求四边形DEBF的周长.
【答案】(1)见解析;(2)12.
【解析】
(1)根据平行四边形的对角相等以及角平分线的定义,证明∠ABF=∠AED,则DE∥BF,即可得到四边形DEBF是平行四边形,根据平行四边形的对角线互相平分即可证得;
(2)证明△ADE是等边三角形,求得AE、DE的长,则BE即可求得,进而求得DEBF的周长.
证明:(1)∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC.
又∵DE,BF分别是∠ADC,∠ABC的平分线,
∴∠ABF=∠CDE.
又∵∠CDE=∠AED,
∴∠ABF=∠AED,
∴DE∥BF,
∵DF∥BE
∴四边形DEBF是平行四边形,
∴EF,BD互相平分.
(2)由(1)知∠ADE=∠AED,
∵∠A=60°,
∴△ADE是等边三角形.
∴AE=DE=AD=4,
又∵AE:EB=2:1,
∴EB=2.
∴四边形DEBF的周长是12.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目