(2011•石家庄二模)(1)在△ABE中.AC⊥BE.垂足为C.点D在AC上.连接BD.ED．如果△ABC∽△EDC.如图1.当BCAC=1时.求证:BD=AE,如图2.当BCAC=k时.请猜想BD与AE的数量关系和位置关系.并证明．(2)如图3.如果△ABC∽△EDC.当BCAC=k时.请直接写出BD与AE的数量关系．题目和参考答案——青夏教育精英家教网—

题目内容

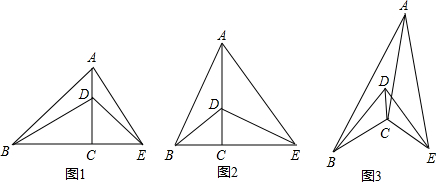
（2011•石家庄二模）（1）在△ABE中，AC⊥BE，垂足为C，点D在AC上，连接BD、ED．
如果△ABC∽△EDC，
如图1，当

=1时，求证：BD=AE；
如图2，当

=k时，请猜想BD与AE的数量关系和位置关系，并证明．
（2）如图3，如果△ABC∽△EDC，当

=k时，请直接写出BD与AE的数量关系．

分析：（1）当

=1时，根据相似三角形的性质得

，易得BC=AC，CD=CE，根据全等三角形的判定可得到Rt△BCD≌Rt△ACE，即可得到结论；
当

=k时，延长BD交AE于点F，根据相似三角形的性质得

，则

，根据相似三角形的判定可得到Rt△BCD∽Rt△ACE，则

，∠BDC=∠AEC，得到BD=kAE，而∠BCD=90°，即可得到∠CBD+∠AEC=90°，即BD⊥AE；
（2）由（1）的第二种情况可推出BD=kAE．

解答：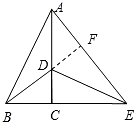

解：（1）当

=1时，
证明：∵△ABC∽△EDC，
∴

，
∴

，
又∵

=1，
∴BC=AC，CD=CE，
又∵AC⊥BE，
∴∠ACB=∠ECD=90°，
∴Rt△BCD≌Rt△ACE，
∴BD=AE；
当

=k时，有BD=kAE，BD⊥AE．
证明如下：如图，延长BD交AE于点F，
∵△ABC∽△EDC，
∴

，
∴

，
又∵AC⊥BE，
∴∠ACB=∠ECD=90°，
∴Rt△BCD∽Rt△ACE，
∴

，∠BDC=∠AEC，
∵

=k，
∴BD=kAE，
∴BD=kAE；
∵∠BCD=90°，
∴∠CBD+∠CDB=90°，
∴∠CBD+∠AEC=90°，
∴BD⊥AE；

（2）BD=kAE．

点评：本题考查了相似三角形的判定与性质：有两组对应边的比相等，并且它们的夹角相等的两三角形相似；相似三角形的对应边比相等．也考查了全等三角形的判定与性质．

练习册系列答案

．

（2011•石家庄二模）阅读材料：
我们将能完全覆盖平面图形的最小圆称为该平面图形的最小覆盖圆．
例如：线段AB的最小覆盖圆就是以线段AB为直径的圆．
操作探究：
（1）如图1：已知线段AB与其外一点C，作过A、B、C三点的最小覆盖圆；（不写作法，保留作图痕迹）
（2）边长为1cm的正方形的最小覆盖圆的半径是

cm；
如图2，边长为1cm的两个正方形并列在一起，则其最小覆盖圆的半径是

cm；
如图3，半径为1cm的两个圆外切，则其最小覆盖圆的半径是

cm．

联想拓展：
⊙O₁的半径为8，⊙O₂，⊙O₃的半径均为5．
（1）当⊙O₁、⊙O₂、⊙O₃两两外切时（如图4），则其最小覆盖圆的半径是

；
（2）当⊙O₁、⊙O₂、⊙O₃两两相切时，（1）中的结论还成立吗？如果不成立，则其最小覆盖圆的半径是

，并作出示意图．

试题分类