题目内容
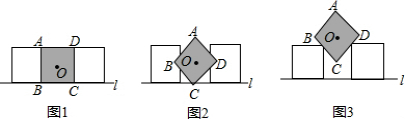
(2011•石家庄二模)三个边长为1的正方形并排放置在直线l上(如图1所示),将中间的正方形绕其中点O旋转45°(如图2),再将其向上平移至图3的位置,使两侧正方形的顶点分别落在BC、CD边上,则点A到直线l的距离为
+
+
.
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |

分析:如图:点A到L的距离为对角线AC的长度加上边长再减去CE的长度.
解答: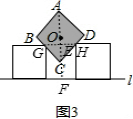 解:由于正方形是旋转45°由正方形的性质可得出:∠CHE=∠CGE=45°,CG=CH;
解:由于正方形是旋转45°由正方形的性质可得出:∠CHE=∠CGE=45°,CG=CH;
又由∠BCD=90°则CH2+CG2=GH2,GH=1.
所以CG=
,
根据面积公式得:GC×CH=CE×GH
所以CE=
;
对角线AC=
,
所以A距l的距离AF=AC+EF-CE=
+
.
故答案为:
+
.
 解:由于正方形是旋转45°由正方形的性质可得出:∠CHE=∠CGE=45°,CG=CH;
解:由于正方形是旋转45°由正方形的性质可得出:∠CHE=∠CGE=45°,CG=CH;又由∠BCD=90°则CH2+CG2=GH2,GH=1.
所以CG=
| ||
| 2 |
根据面积公式得:GC×CH=CE×GH
所以CE=
| 1 |
| 2 |
对角线AC=
| 2 |
所以A距l的距离AF=AC+EF-CE=
| 2 |
| 1 |
| 2 |
故答案为:
| 2 |
| 1 |
| 2 |
点评:考查了正方形的性质和旋转的性质,此题重点在于作出图形,由题意得出∠CHE=∠CGE=45°,通过勾股定理和面积公式得出CE的长度.

练习册系列答案
相关题目