题目内容
 (2011•抚顺一模)如图,抛物线y=
(2011•抚顺一模)如图,抛物线y=| 1 | 2 |
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)若点M(0,-4),动点P从M点出发,沿直线运动到该抛物线对称轴的某点E,再沿直线运动到x轴上某点F,最后沿直线运动到点C,求使点P运动的总路程最短的点E、点F的坐标,并求出这个最短路程的长.
分析:(1)利用待定系数法求二次函数解析式,进而利用配方法求出顶点坐标即可;
(2)根据点的坐标得出AC 2=AO 2+CO2=1+4=5,BC 2=BO 2+CO2=16+4=20,AB 2=(AO+BO)2=25,即可得出△ABC的形状;
(3)作C关于x=
的对称点C′,M关于x轴对称点M′,连接M′C′交x轴于点F、抛物线对称轴于点E,利用勾股定理求出即可,或者做M点关于抛物线对称轴的对称点M′(3,-4),做C点关于x轴的对称点C′(0,2),连接M'C',进而得出即可.
(2)根据点的坐标得出AC 2=AO 2+CO2=1+4=5,BC 2=BO 2+CO2=16+4=20,AB 2=(AO+BO)2=25,即可得出△ABC的形状;
(3)作C关于x=
| 3 |
| 2 |
解答:解:(1)∵抛物线y=
x2+bx-2经过A(-1,0),
∴0=
-b-2,
解得:b=-
,
∴y=
x2-
x-2,
∵y=
x2-
x-2=
(x2-3x)-2=
(x-
)2-
,
∴顶点D的坐标为:(
,-
);
(2)当x=0,∴y=-2,
∴C点坐标为:(0,-2),
∴y=
x2-
x-2与x轴交于A、B,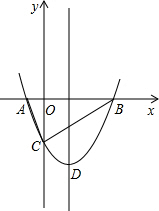
∴0=
x2-
x-2,
解得:x1=-1,x2=4,
∴B点坐标为:(4,0),
∴AC 2=AO 2+CO2=1+4=5,
BC 2=BO 2+CO2=16+4=20,
AB 2=(AO+BO)2=25,
∴AC 2+BC 2=AB2,
∴△ABC的形状是直角三角形;
(3)①作C关于x=
的对称点C′,
M关于x轴对称点M′,连接M′C′交x轴于点F、抛物线对称轴于点E,
则有:MF+FE+EC为点P运动的最短路程,
求出直线M′C′:y=-2x+4,
求出点F(2,0),点E(
,1),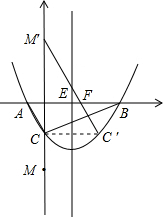
最短路线为:3
.
②做M点关于抛物线对称轴的对称点M′(3,-4),
做C点关于x轴的对称点C′(0,2),
连接M'C',则M'C'长度即为所求最小长度3
;
M'C'与x轴交点为所求F点,
而M'C'与抛物线对称轴的交点为所求E点,
F点坐标(1,0),
E点坐标(1.5,-1).
| 1 |
| 2 |
∴0=
| 1 |
| 2 |
解得:b=-
| 3 |
| 2 |
∴y=
| 1 |
| 2 |
| 3 |
| 2 |
∵y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
∴顶点D的坐标为:(
| 3 |
| 2 |
| 25 |
| 8 |
(2)当x=0,∴y=-2,
∴C点坐标为:(0,-2),
∴y=
| 1 |
| 2 |
| 3 |
| 2 |

∴0=
| 1 |
| 2 |
| 3 |
| 2 |
解得:x1=-1,x2=4,
∴B点坐标为:(4,0),
∴AC 2=AO 2+CO2=1+4=5,
BC 2=BO 2+CO2=16+4=20,
AB 2=(AO+BO)2=25,
∴AC 2+BC 2=AB2,
∴△ABC的形状是直角三角形;
(3)①作C关于x=
| 3 |
| 2 |
M关于x轴对称点M′,连接M′C′交x轴于点F、抛物线对称轴于点E,
则有:MF+FE+EC为点P运动的最短路程,
求出直线M′C′:y=-2x+4,
求出点F(2,0),点E(
| 3 |
| 2 |

最短路线为:3
| 5 |
②做M点关于抛物线对称轴的对称点M′(3,-4),
做C点关于x轴的对称点C′(0,2),
连接M'C',则M'C'长度即为所求最小长度3
| 5 |
M'C'与x轴交点为所求F点,
而M'C'与抛物线对称轴的交点为所求E点,
F点坐标(1,0),
E点坐标(1.5,-1).
点评:此题主要考查了二次函数的综合应用和最短路径问题以及直角三角形的判定方法等知识,根据已知结合图象得出最短路径求法是解题关键.

练习册系列答案
相关题目
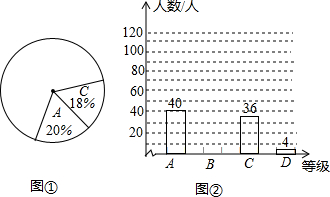 中“比较了解”垃圾分类知识的人数约为多少人?
中“比较了解”垃圾分类知识的人数约为多少人? (2011•抚顺一模)如图,已知Rt△ABC,∠ABC=90°.
(2011•抚顺一模)如图,已知Rt△ABC,∠ABC=90°.