题目内容
 (2011•抚顺一模)如图,已知Rt△ABC,∠ABC=90°.
(2011•抚顺一模)如图,已知Rt△ABC,∠ABC=90°.(1)根据下列语句作图并保留作图痕迹:作Rt△ABC的外接圆⊙O,过点A作⊙O的切线PA与AB的垂直平分线交于点P.
(2)连接PB,求证:PB是⊙O的切线;
(3)已知PA=AB=
| 3 |
分析:(1)利用直角三角形外接圆的性质,直接找到斜边中点求出即可;
(2)利用切线的性质与判定,得出∠OAB+∠BAP=∠OBA+∠PBA=90°,即可得出答案;
(3)根据(2)中所求,可以得出△PAB是等边三角形,进而得出r=1,∠AOB=60°,∠AOB=120°,即可求出所求图形的面积.
(2)利用切线的性质与判定,得出∠OAB+∠BAP=∠OBA+∠PBA=90°,即可得出答案;
(3)根据(2)中所求,可以得出△PAB是等边三角形,进而得出r=1,∠AOB=60°,∠AOB=120°,即可求出所求图形的面积.
解答:(1)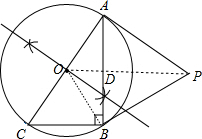 解:如图所示:
解:如图所示:
(2)证明:∵点P、O在AB垂直平分线上,
∴PA=PB,AO=BO,
∴∠PAB=∠PBA,
∠OAB=∠OBA,
∵PA是⊙O的切线,
∴∠OAP=90°,
∴∠OAB+∠BAP=∠OBA+∠PBA=90°,
∴OB⊥PB,
∴PB是⊙O切线;
(3)解:∵PA,PB都是⊙O的切线,
∴PA=PB,
∵PA=AB=
,
∴PA=AB=PB,
∴△PAB是等边三角形,
∴∠PAD=60°,
∴∠OAD=30°,
∴r=1,∠AOB=60°,∠AOB=120°,
∴S四边形AOBP=
×1×
×2=
,
S扇形AOB=
π,
所求图形的面积为(
-
π)平方厘米.
 解:如图所示:
解:如图所示:(2)证明:∵点P、O在AB垂直平分线上,
∴PA=PB,AO=BO,
∴∠PAB=∠PBA,
∠OAB=∠OBA,
∵PA是⊙O的切线,
∴∠OAP=90°,
∴∠OAB+∠BAP=∠OBA+∠PBA=90°,
∴OB⊥PB,
∴PB是⊙O切线;
(3)解:∵PA,PB都是⊙O的切线,
∴PA=PB,
∵PA=AB=
| 3 |
∴PA=AB=PB,
∴△PAB是等边三角形,
∴∠PAD=60°,
∴∠OAD=30°,
∴r=1,∠AOB=60°,∠AOB=120°,
∴S四边形AOBP=
| 1 |
| 2 |
| 3 |
| 3 |
S扇形AOB=
| 1 |
| 3 |
所求图形的面积为(
| 3 |
| 1 |
| 3 |
点评:此题主要考查了切线的判定与性质以及扇形面积求法和做复杂图形,根据已知得出正确图形是解题关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
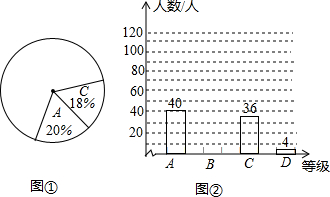 中“比较了解”垃圾分类知识的人数约为多少人?
中“比较了解”垃圾分类知识的人数约为多少人?
 (2011•抚顺一模)如图,抛物线y=
(2011•抚顺一模)如图,抛物线y=