题目内容
阅读下列材料并解决有关问题:
我们知道: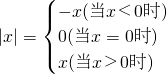 ,现在我们可以用这一结论来解含有绝对值的方程.例如,解方程|x+1|+|2x-3|=8时,可令x+1=0和2x-3=0,分别求得x=-1和,(称-1和
,现在我们可以用这一结论来解含有绝对值的方程.例如,解方程|x+1|+|2x-3|=8时,可令x+1=0和2x-3=0,分别求得x=-1和,(称-1和 分别为|x+1|和|2x-3|的零点值),在实数范围内,零点值x=-1和可将全体实数分成不重复且不遗漏的如下3种情况:①x<-1②
分别为|x+1|和|2x-3|的零点值),在实数范围内,零点值x=-1和可将全体实数分成不重复且不遗漏的如下3种情况:①x<-1②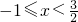 ③
③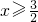 ,从而解方程|x+1|+|2x-3|=5可分以下三种情况:
,从而解方程|x+1|+|2x-3|=5可分以下三种情况:
①当x<-1时,原方程可化为-(x+1)-(2x-3)=8,解得x=-2.
②当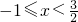 时,原方程可化为(x+1)-(2x-3)=8,解得x=-4,但不符合
时,原方程可化为(x+1)-(2x-3)=8,解得x=-4,但不符合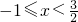 ,故舍去.
,故舍去.
③当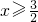 时,原方程可化为(x+1)+(2x-3)=8,解得
时,原方程可化为(x+1)+(2x-3)=8,解得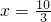 .
.
综上所述,方程|x+1|+|2x-3|=8的解为,x=-2和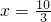 .
.
通过以上阅读,请你解决以下问题:
(1)分别求出|x+2|和|3x-1|的零点值.
(2)解方程|x+2|+|3x-1|=9.
解:(1)令x+2=0,
解得:x=-2,
3x-1=0
解得:x= ,
,
∴|x+2|的零点值为-2.|3x-1|的零点值为 ;
;
(2)解:①∵当x<-2时,-(x+2)-(3x-1)=9
∴x=-
②∵当-2≤x< 时,(x+2)-(3x-1)=9,
时,(x+2)-(3x-1)=9,
∴x=-3,但不符合-2≤x< ,故舍去.
,故舍去.
③∵当x≥ 时,(x+2)+(3x-1)=9,
时,(x+2)+(3x-1)=9,
∴x=2
∴方程|x+2|+|3x-1|=9的解为x1=- ,x2=2.
,x2=2.
分析:(1)分别求方程x+2=0,3x-1=0的解即可;
(2)分为三个阶段:①当x<-2时,方程化为:-(x+2)-(3x-1)=9,求出方程的解即可;②当-2≤x< 时,方程化为(x+2)-(3x-1)=9,求出方程的解即可;③当x≥
时,方程化为(x+2)-(3x-1)=9,求出方程的解即可;③当x≥ 时,方程化为(x+2)+(3x-1)=9,求出方程的解即可.
时,方程化为(x+2)+(3x-1)=9,求出方程的解即可.
点评:本题考查了含绝对值符号的一元一次方程和绝对值的应用,注意:求此类方程时,先求出零点值,再看看分成几个阶段,求出每一阶段的方程的解即可,注意:一定要看看求出的数是否满足x的范围.
解得:x=-2,
3x-1=0
解得:x=
 ,
,∴|x+2|的零点值为-2.|3x-1|的零点值为
 ;
;(2)解:①∵当x<-2时,-(x+2)-(3x-1)=9
∴x=-

②∵当-2≤x<
 时,(x+2)-(3x-1)=9,
时,(x+2)-(3x-1)=9,∴x=-3,但不符合-2≤x<
 ,故舍去.
,故舍去.③∵当x≥
 时,(x+2)+(3x-1)=9,
时,(x+2)+(3x-1)=9,∴x=2
∴方程|x+2|+|3x-1|=9的解为x1=-
 ,x2=2.
,x2=2.分析:(1)分别求方程x+2=0,3x-1=0的解即可;
(2)分为三个阶段:①当x<-2时,方程化为:-(x+2)-(3x-1)=9,求出方程的解即可;②当-2≤x<
 时,方程化为(x+2)-(3x-1)=9,求出方程的解即可;③当x≥
时,方程化为(x+2)-(3x-1)=9,求出方程的解即可;③当x≥ 时,方程化为(x+2)+(3x-1)=9,求出方程的解即可.
时,方程化为(x+2)+(3x-1)=9,求出方程的解即可.点评:本题考查了含绝对值符号的一元一次方程和绝对值的应用,注意:求此类方程时,先求出零点值,再看看分成几个阶段,求出每一阶段的方程的解即可,注意:一定要看看求出的数是否满足x的范围.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
 nB,AD=bsinC,于是csinB=bsinC,即
nB,AD=bsinC,于是csinB=bsinC,即 到0.1.参考数据:sin40°=0.643,sin65°=0.90 6,sin70°=0.940,sin75°=0.966).
到0.1.参考数据:sin40°=0.643,sin65°=0.90 6,sin70°=0.940,sin75°=0.966).