��Ŀ����
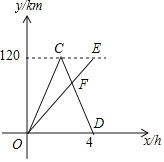
����Ŀ��ij�̳����۲�ƷA����һ����ƷA����40����ȫ�����꣮���̳��Ե�һ����ƷA���к��������������˸��ٵ��飬��������ͼ��ʾ��ͼ���е����߱�ʾ��������w������ʱ��t�Ĺ�ϵ��ͼ���е����߱�ʾÿ����ƷA����������y������ʱ��t�Ĺ�ϵ��
��1���۲�ͼ�٣���д����һ����ƷA����������w������ʱ��t�Ĺ�ϵ��
��2����һ����ƷA���к���һ������̵�����������Q�������������Q����Ƕ���Ԫ��������������ÿ����ƷA����������������������
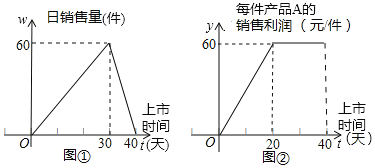
���𰸡���1����0��t��30ʱ����������w��2t����30��t��40ʱ����������w����6t+240����2����һ����ƷA���к�30�죬����̵�����������Q�������������Q�����3600Ԫ��
��������
��1����������ͺ���ͼ���е����ݿ�����õ�һ����ƷA����������w������ʱ��t�Ĺ�ϵ��
��2�����ݺ���ͼ���е����ݿ�����õ�һ����ƷA���к���һ������̵�����������Q������Q�����ֵ��
�⣺��1����ͼ���ɵã�
��0��t��30ʱ��������������w��kt��
���㣨30��60����ͼ���ϣ�
��60��30k��
��k��2����w��2t��
��30��t��40ʱ��������������w��k1t+b��
���㣨30��60���ͣ�40��0����ͼ���ϣ�
��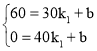 ��
��
��ã�k1����6��b��240��
��w����6t+240��
������������������w��![]() ��
��
����0��t��30ʱ����������w��2t����30��t��40ʱ����������w����6t+240��
��2����ͼ��֪����t��30���죩ʱ����������w�ﵽ������ֵw��60��
����ͼ��֪����t��30���죩ʱ����ƷA������������y�ﵽ������ֵy��60��Ԫ/������
����t��30���죩ʱ��������������Q����������������Q��60��60��3600��Ԫ����
�𣺵�һ����ƷA���к�30�죬����̵�����������Q�������������Q�����3600Ԫ��

 Ŀ�����ϵ�д�
Ŀ�����ϵ�д�