题目内容
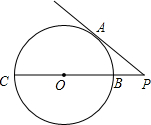如图，PA与⊙O相切于点A，PC经过⊙O的圆心且与该圆相交于两点B、C，若PA=4，PB=2，则sinP=分析：连接OA，先利用勾股定理求出⊙O的半径长，再根据三角函数的定义解答即可．
解答：
解：连接OA，设⊙O的半径为r，则OP=OB+BP=r+2，
因为PA与⊙O相切于点A，所以OA⊥AP，
根据勾股定理得，OP2=OA2+AP2，即（r+2）2=r2+42，解得，r=3，
故sinP=
=
=
．
解：连接OA，设⊙O的半径为r，则OP=OB+BP=r+2，因为PA与⊙O相切于点A，所以OA⊥AP，
根据勾股定理得，OP2=OA2+AP2，即（r+2）2=r2+42，解得，r=3，
故sinP=
| OA |
| OB+BP |
| 3 |
| 3+2 |
| 3 |
| 5 |
点评：此题比较简单，解答此题的关键是连接OA，利用切线的性质构造出直角三角形，再根据三角函数的定义解答即可．
练习册系列答案
阅读快车系列答案
相关题目
如图，PA与⊙O相切于A点，弦AB⊥OP，垂足为C，OP与⊙O相交于D点，已知OA=2，OP=4．
23、如图，PA与⊙O相切，切点为A，PO交⊙O于点C，点B是优弧CBA上一点，若∠ABC=32°，则∠P的度数为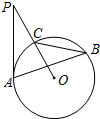
（2012•郑州模拟）如图，PA与⊙O相切，切点为A，PO交⊙O于点C，点B是优弧
如图，PA与⊙O相切于点A，PO的延长线与⊙O交于点C，若⊙O的半径为3，PA=4．弦AC的长为