题目内容
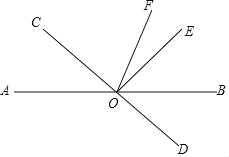
【题目】如图,直线AB,CD交于点O,OB平分∠DOE,OF是∠BOC的角平分线.
(1)说明:∠AOC=∠BOE;
(2)若∠AOC=46°,求∠EOF的度数;
(3)若∠EOF=30°,求∠AOC的度数.
【答案】(1)证明见解析;(2)∠EOF=21°;(3)∠AOC=40°.
【解析】
(1)根据角平分线的定义得到∠BOE=∠BOD,根据角的和差即可得到结论;
(2)根据邻补角的定义得到∠BOC=180°﹣∠AOC=134°,∠BOE=46°,根据角平分线的定义得到∠BOF=![]() ∠BOC=67°,于是得到结论;
∠BOC=67°,于是得到结论;
(3)设∠AOC=α,则∠BOE=α,得到∠BOF=α+30°,由OF是∠BOC的角平分线,得到∠BOC=2∠BOF=2α+60°,于是得到结论.
解:(1)∵OB平分∠DOE,
∴∠BOE=∠BOD,
∵∠AOC=∠BOD,
∴∠AOC=∠BOE;
(2)∵∠AOC=46°,
∴∠BOC=180°﹣∠AOC=134°,∠BOE=46°,
∵OF是∠BOC的角平分线,
∴∠BOF=![]() ∠BOC=67°,
∠BOC=67°,
∴∠EOF=∠BOF﹣∠BOE=21°;
(3)设∠AOC=α,则∠BOE=α,
∵∠EOF=30°,
∴∠BOF=α+30°,
∵OF是∠BOC的角平分线,
∴∠BOC=2∠BOF=2α+60°,
∴α=180°﹣(2α+60°),
∴α=40°,
∴∠AOC=40°.

 阅读快车系列答案
阅读快车系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制成如下统计图表(单位:cm):
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
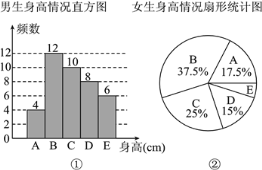
根据图表提供的信息,样本中,身高在160≤x<170之间的女生人数为( )
A. 8 B. 6 C. 14 D. 16



