题目内容
【题目】(1)如图1:已知△ABC中,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE、CD,请你完成图形(尺规作图,不写作法.但要保留作图痕迹).
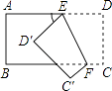
(2)如图2,已知△ABC中,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE、CD,判断BE与CD有什么数量关系,并加以证明.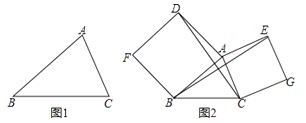
【答案】解:(1)如图所示: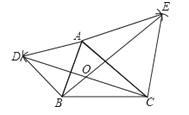
(2)解:CD=BE.
理由如下:
∵四边形ABFD和四边形ACGE都是正方形,
∴AD=AB,AC=AE,∠DAB=∠CAE=90°,
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE.
在△ADC和△ABE中,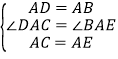 ,
,
∴△ADC≌△ABE(SAS),
∴CD=BE.
【解析】(1)分别以A、B为圆心,AB长为半径画弧,两弧交于点D,连接AD,BD,同理连接AE,CE即可;
(2)BE与CD数量关系是相等,由正方形的性质就可以得出△ADC≌△ABE,根据全等三角形的性质即可得到CD=BE.
【考点精析】根据题目的已知条件,利用等边三角形的性质的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目