题目内容
抛物线 与
与 轴交于点A,B,与y轴交于点C,其中点B的坐标为
轴交于点A,B,与y轴交于点C,其中点B的坐标为 .
.
(1)求抛物线对应的函数表达式;]
(2)将(1)中的抛物线沿对称轴向上平移,使其顶点M落在线段BC上,记该抛物线为G,求抛物线G所对应的函数表达式;
(3)将线段BC平移得到线段 (B的对应点为
(B的对应点为 ,C的对应点为
,C的对应点为 ),使其经过(2)中所得抛物线G的顶点M,且与抛物线G另有一个交点N,求点
),使其经过(2)中所得抛物线G的顶点M,且与抛物线G另有一个交点N,求点 到直线
到直线 的距离
的距离 的取值范围.
的取值范围.
(1)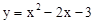 ;(2)
;(2)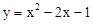 ;(3)
;(3)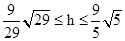 .
.
解析试题分析:(1)根据曲线上点的坐标与方程的关系,将B 代入
代入 求出k即可.
求出k即可.
(2)应用待定系数法求出直线BC的解析式,将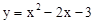 对称轴的
对称轴的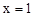 代入BC的解析式求得抛物线G的顶点坐标,从而得到抛物线G所对应的函数表达式.
代入BC的解析式求得抛物线G的顶点坐标,从而得到抛物线G所对应的函数表达式.
(3)连接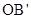 ,过点
,过点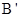 作
作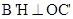 于点H,由
于点H,由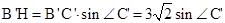 知当
知当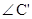 最大时h最大,当
最大时h最大,当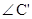 最小时h最小.,即当
最小时h最小.,即当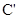 与M重合时,
与M重合时,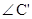 最大,h最大;当
最大,h最大;当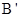 与M重合时,
与M重合时,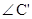 最小,h最小,据此求解即可.
最小,h最小,据此求解即可.
试题解析:(1)将B 代入
代入 得
得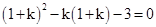 ,解得
,解得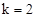 .
.
∴抛物线对应的函数表达式为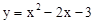 .
.
(2)由题意得,B(3,0),C(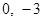 ).
).
∴直线BC的解析式为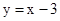 .
.
由(1)得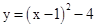 ,
,
∵将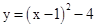 的图象向上平移时,横坐标不变,
的图象向上平移时,横坐标不变,
∴将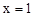 代入
代入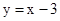 得
得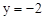 .
.
∴抛物线G的顶点坐标为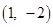 。
。
∴抛物线G所对应的函数表达式为 ,即
,即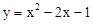 .
.
(3)如图1,连接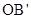 ,过点
,过点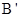 作
作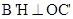 于点H,
于点H,
∵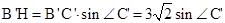 ,
,
∴当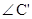 最大时h最大,当
最大时h最大,当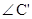 最小时h最小.
最小时h最小.
由图1可知当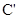 与M重合时,
与M重合时,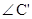 最大,h最大.
最大,h最大.
此时,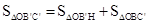 ,即
,即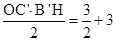 ,∴
,∴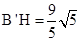 .
.
由图2可知当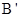 与M重合时,
与M重合时,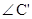 最小,h最小.
最小,h最小.
此时,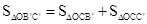 ,即
,即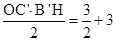 ,
,
此时,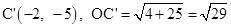 ,∴
,∴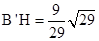 .
.
综上所述,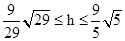 .
.
考点:1.二次函数综合题;2.平移的性质;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.二次函数的性质;6.三角形的面积;7.转换思想的应用.

练习册系列答案
相关题目
 )作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
)作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.


 .
. ﹣m(0<m<
﹣m(0<m< 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C. 是等腰三角形,求抛物线的解析式;
是等腰三角形,求抛物线的解析式; ,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线
,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线 时,点M位于点N的下方,求这个一次函数的解析式.
时,点M位于点N的下方,求这个一次函数的解析式.
 中,矩形
中,矩形 的边
的边 在
在 轴上,且
轴上,且 ,
, ,直线
,直线 经过点
经过点 ,交
,交 轴于点
轴于点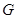 .
. 的坐标分别是
的坐标分别是 的抛物线的解析式;
的抛物线的解析式; ,顶点为点
,顶点为点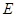 .求出当
.求出当 时抛物线的解析式.
时抛物线的解析式.

 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点. DQ,求点F的坐标.
DQ,求点F的坐标.
