题目内容
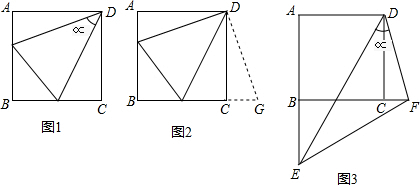
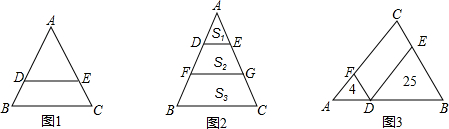
(1)如图1,已知DE∥BC,DE平分△ABC的面积,直接写出AD:BD=
(2)如图2,已知DE∥FG∥BC,点D、F是线段AB的三等分点,记△ADE、四边形DFGE和四边形FBCG的面积分别为S1、S2、S3,求S1:S2:S3的值;
(3)如图3,已知D、E、F分别位于△ABC的三边上,且四边形CEDF为平行四边形,△ADF和△BDE的面积分别为4和25,求四边形CEDF的面积.
(
+1):1
| 2 |
(
+1):1
;| 2 |
(2)如图2,已知DE∥FG∥BC,点D、F是线段AB的三等分点,记△ADE、四边形DFGE和四边形FBCG的面积分别为S1、S2、S3,求S1:S2:S3的值;
(3)如图3,已知D、E、F分别位于△ABC的三边上,且四边形CEDF为平行四边形,△ADF和△BDE的面积分别为4和25,求四边形CEDF的面积.

分析:(1)先根据DE∥BC得出△ADE∽△ABC,再根据DE平分△ABC的面积得出
的值,故可得出结论;
(2)由点D、F是线段AB的三等分点,可得DE∥FG∥BC,AD:AF:AB=1:2:3,即可证得△ADE∽△AFG∽△ABC,然后由相似三角形面积比等于相似比的平方,求得S△ADE:S△AFG:S△ABC的值,继而求得答案;
(3)连接CD,先根据相似三角形的判定定理得出△AFD∽△DEB,再根据相似三角形的对应边成比例得出
的值,可得出△CED的面积,进而可得出结论.
| AD |
| AB |
(2)由点D、F是线段AB的三等分点,可得DE∥FG∥BC,AD:AF:AB=1:2:3,即可证得△ADE∽△AFG∽△ABC,然后由相似三角形面积比等于相似比的平方,求得S△ADE:S△AFG:S△ABC的值,继而求得答案;
(3)连接CD,先根据相似三角形的判定定理得出△AFD∽△DEB,再根据相似三角形的对应边成比例得出
| DF |
| BE |
解答:解:(1)∵DE∥BC,
∴△ADE∽△ABC,
∵DE平分△ABC的面积,
∴
=
=
,
∴
=
=
=(
+1):1.
故答案为:(
+1):1;
(2)∵点D、F是线段AB的三等分点,
∴DE∥FG∥BC,AD:AF:AB=1:2:3,
∴△ADE∽△AFG∽△ABC,
∴S△ADE:S△AFG:S△ABC=1:4:9,
∴S1:S2:S3=1:3:5.
(3)连接CD,
∵四边形CEDF为平行四边形,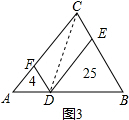
∴DE∥AC,DF∥BC,
∴∠A=∠BDE,∠AFD=∠DEB,
∴△AFD∽△DEB,
∵△ADF和△BDE的面积分别为4和25,
∴
=
=
=
=
,
∴
=
,
∴S△CED=25×
=10
∴S四边形CEDF=2×S△CED=20.
∴△ADE∽△ABC,
∵DE平分△ABC的面积,
∴
| AD |
| AB |
|
| ||
| 2 |
∴
| AD |
| BD |
| AD |
| AB-AD |
| ||
2-
|
| 2 |
故答案为:(
| 2 |
(2)∵点D、F是线段AB的三等分点,
∴DE∥FG∥BC,AD:AF:AB=1:2:3,
∴△ADE∽△AFG∽△ABC,
∴S△ADE:S△AFG:S△ABC=1:4:9,
∴S1:S2:S3=1:3:5.
(3)连接CD,
∵四边形CEDF为平行四边形,

∴DE∥AC,DF∥BC,
∴∠A=∠BDE,∠AFD=∠DEB,
∴△AFD∽△DEB,
∵△ADF和△BDE的面积分别为4和25,
∴
| DF |
| BE |
|
|
| 2 |
| 5 |
| CE |
| BE |
∴
| S△CED |
| S△DEB |
| 2 |
| 5 |
∴S△CED=25×
| 2 |
| 5 |
∴S四边形CEDF=2×S△CED=20.
点评:本题考查的是相似三角形的判定与性质,熟知相似三角形边长的比等于相似比,面积的比等于相似比的平方是解答此题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 下列说法:
下列说法: