题目内容
如图,将边长为12cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B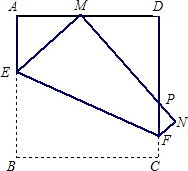 落在AD边上的点M处,点C落在点N处,MN与CD交于点P.
落在AD边上的点M处,点C落在点N处,MN与CD交于点P.
(1)若AM=5,①求AE的长;②求折痕EF的长.
(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.
解:(1)①设AE=x,由折叠的性质可知EM=BE=12-x,
在Rt△AEM中,由勾股定理,得AE2+AM2=EM2,即x2+52=(12-x)2,
解得x=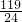 ,即AE=
,即AE=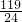 cm;
cm;
②过点F作FG⊥AB,垂足为G,连接BM,
∵四边形ABCD是正方形,
∴AB=BC,
∵四边形BCFG是矩形,
∴FG=BC,
∴AB=FG,
∵BM⊥FE,
∴∠EBM+∠BEF=90°,
∵∠BMA+∠EBM=90°,
∠BEF=∠BMA,
又∵∠A=∠EGF=90°,
∴△ABM≌△GFE,
∴EF=BM=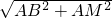 =
=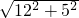 =13cm;
=13cm;
(2)△PDM的周长不变,为24cm.
理由:设AE=x,AM=y,则BE=EM=12-x,MD=12-y,
在Rt△AEM中,由勾股定理得AE2+AM2=EM2,
x2+y2=(12-x)2,解得144-y2=24x,
∵∠EMP=90°,∠A=∠D,
∴Rt△AEM∽Rt△DMP,
∴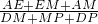 =
=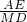 ,即
,即 =
=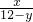 ,
,
解得DM+MP+DP=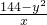 =24.
=24.
分析:(1)①设AE=x,由折叠的性质可知EM=BE=12-x,在Rt△AEM中,运用勾股定理求AE;②过点F作FG⊥AB,垂足为G,连接BM,根据折叠的性质得点B和点M关于EF对称,即BM⊥EF,又AB=FG,∠A=∠EGF=90°,可证△ABM≌△GFE,把求EF的问题转化为求BM;
(2)设AE=x,AM=y,则BE=EM=12-x,MD=12-y,在Rt△AEM中,由勾股定理得出x、y的关系式,可证Rt△AEM∽Rt△DMP,根据相似三角形的周长比等于相似比求△DMP的周长.
点评:本题考查了折叠的性质.关键是根据折叠前后对应线段相等怎么全等三角形,根据角的互余关系证明相似三角形,结合勾股定理,相似三角形的性质解题.
在Rt△AEM中,由勾股定理,得AE2+AM2=EM2,即x2+52=(12-x)2,
解得x=
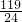 ,即AE=
,即AE=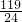 cm;
cm;②过点F作FG⊥AB,垂足为G,连接BM,

∵四边形ABCD是正方形,
∴AB=BC,
∵四边形BCFG是矩形,
∴FG=BC,
∴AB=FG,
∵BM⊥FE,
∴∠EBM+∠BEF=90°,
∵∠BMA+∠EBM=90°,
∠BEF=∠BMA,
又∵∠A=∠EGF=90°,
∴△ABM≌△GFE,
∴EF=BM=
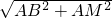 =
=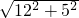 =13cm;
=13cm;(2)△PDM的周长不变,为24cm.
理由:设AE=x,AM=y,则BE=EM=12-x,MD=12-y,
在Rt△AEM中,由勾股定理得AE2+AM2=EM2,
x2+y2=(12-x)2,解得144-y2=24x,
∵∠EMP=90°,∠A=∠D,
∴Rt△AEM∽Rt△DMP,
∴
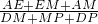 =
=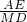 ,即
,即 =
=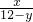 ,
,解得DM+MP+DP=
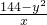 =24.
=24.分析:(1)①设AE=x,由折叠的性质可知EM=BE=12-x,在Rt△AEM中,运用勾股定理求AE;②过点F作FG⊥AB,垂足为G,连接BM,根据折叠的性质得点B和点M关于EF对称,即BM⊥EF,又AB=FG,∠A=∠EGF=90°,可证△ABM≌△GFE,把求EF的问题转化为求BM;
(2)设AE=x,AM=y,则BE=EM=12-x,MD=12-y,在Rt△AEM中,由勾股定理得出x、y的关系式,可证Rt△AEM∽Rt△DMP,根据相似三角形的周长比等于相似比求△DMP的周长.
点评:本题考查了折叠的性质.关键是根据折叠前后对应线段相等怎么全等三角形,根据角的互余关系证明相似三角形,结合勾股定理,相似三角形的性质解题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 边长为1的正方形OA1B1C1的顶点A1在x轴的正半轴上,如图将正方形OA1B1C1绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图象上,则a的值为( )
边长为1的正方形OA1B1C1的顶点A1在x轴的正半轴上,如图将正方形OA1B1C1绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图象上,则a的值为( )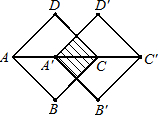 如图,将边长为
如图,将边长为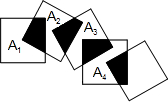 如图,将边长都为1cm的正方形按如图所示摆放,点A1、A2、A3、A4分别是正方形的中心,则前5个这样的正方形重叠部分的面积和为( )
如图,将边长都为1cm的正方形按如图所示摆放,点A1、A2、A3、A4分别是正方形的中心,则前5个这样的正方形重叠部分的面积和为( )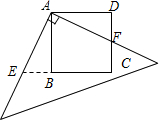 如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角形板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是( )
如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角形板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是( )