题目内容
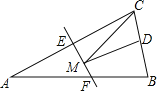
【题目】右图为手的示意图,在各个手指之间标记字母A,B,C,D。请你按图中箭头所指的方向(即A→B→C→D→C→B→A→B→C→……的方式)从A开始数连续的正整数1,2,3,4,5,6,7,8,9,……

(1)当数到14时,对应的字母是_________;
(2)当字母C第201次出现时。恰好数到的数是_________;
(3)当字母C第2n+1次出现时(n为正整数),恰好数到的数是__________(用含有n的代数式表示)
【答案】B. 603. ![]()
【解析】
(1)观察规律,便不难发现六个字母一组,后面不断重复,然后写出答案即可;
(2)每一组字母C出现2次,然后根据C第201次出现,则共有100组,在101组中第三个数字出现,即可进行解答.
(3)根据题意,当字母C第2n+1次出现时(n为正整数),恰好数到的数是6n+3.即可得到答案.
解:(1)根据题意,可知:六个字母一组,后面不断重复,
∴![]() ……2,
……2,
∴当数到14时,对应的字母是:B.
故答案为:B.
(2)∵每一组六个字母中,C出现2次,
∴![]() ……1,
……1,
∴当字母C第201次出现时,是第101组第三个位置,
∴恰好数到的数是:![]() ;
;
故答案为:603;
(3)当n=1时,2n+1=3,则C第三次出现,数字为:![]() ;
;
当n=2时,2n+1=5,则C第五次出现,数字为:![]() ;
;
……
当字母C第2n+1次出现时(n为正整数),恰好数到的数是:6n+3.
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=![]() [
[![]() ])
])