题目内容

如图，请在下列四个等式中，选出两个作为条件，推出△AED是等腰三角形，并予以证明．（写出一种即可）
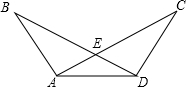
等式：①AB=DC，②BE=CE，③∠B=∠C，④∠BAE=∠CDE．精英家教网
已知：
求证：△AED是等腰三角形．
证明：
分析：根据等腰三角形的判定方法，即在一三角形中等边对等角或等角对等边，可选①③来证明△ABE≌△DCE，从而得到AE=DE，即△AED是等腰三角形．
（或①④，或②③，或②④．）
解答：解：已知：①③（或①④，或②③，或②④）
证明：在△ABE和△DCE中
∵
∠B=∠C
∠AEB=∠DEC
AB=DC

∴△ABE≌△DCE；
∴AE=DE；
△AED是等腰三角形．
点评：此题考查学生对等腰三角形的判定方法及全等三角形的判定的掌握情况；发现并利用全等三角形是正确解答本题的关键．
练习册系列答案
相关题目
阅读：如图1，在△ABC和△DEF中，∠ABC=∠DEF=90°，AB=DE=a，BC=EF=b（a＜b），B、C、D、E四点都在直线m上，点B与点D重合．
连接AE、FC，我们可以借助于S△ACE和S△FCE的大小关系证明不等式：a2+b2＞2ab（b＞a＞0）．
证明过程如下：
∵BC=b，BE=a，EC=b-a．
∴S△ACE=
1
2
EC•AB=
1
2
(b-a)a，S△FCE=
1
2
EC•FE=
1
2
(b-a)b．
∵b＞a＞0
∴S△FCE＞S△ACE
即
1
2
(b-a)b＞
1
2
(b-a)a
∴b2-ab＞ab-a2
∴a2+b2＞2ab
解决下列问题：
（1）现将△DEF沿直线m向右平移，设BD=k（b-a），且0≤k≤1．如图2，当BD=EC时，k=
 
．利用此图，仿照上述方法，证明不等式：a2+b2＞2ab（b＞a＞0）．
（2）用四个与△ABC全等的直角三角形纸板进行拼接，也能够借助图形证明上述不等式．请你画出一个示意图，并简要说明理由．
精英家教网
16、如图，把边长为2cm的正方形剪成四个全等的直角三角形，请用这四个直角三角形拼成符合下列要求的图形．（全部用上，互不重合且不留空隙），并把你的拼法依照图示按实际大小画在方格内（方格为1cm×1cm）
（1）不是正方形的菱形；（一个）
（2）不是正方形的矩形；（一个）
（3）梯形；（一个）
（4）不是矩形和菱形的平行四边形；（一个）
（5）不是梯形和平行四边形的凸四边形；（一个）
（6）与以上画出的图形不全等的其他凸四边形；（画出的图形互不全等，能画出几个画几个，至少画三个）
（7）画凸多边形．（与上面画的图形不一样）
24、如图，把长为2cm的正方形剪成四个全等的直角三角形，请用这四个直角三角形（全部用上）拼成下列符合要求的图形（互不重叠且没有空隙），并把你的拼法画在下列的方格纸内（方格为1cm×1cm）
（1）画一个不是正方形的菱形； 
（2）画一个不是正方形的矩形
（3）画一个不是矩形也不是菱形的平行四边形
 （4）画一个梯形
如图，在?ABCD中，分别以AB、AD为边向外作等边△ABE、△ADF，延长CB交AE于点G，点G在点A，
E之间，连接CE、CF、EF，有下列四个结论：
①△CDF≌△EBC；     ②∠CDF=∠EAF；
③△ECF是等边三角形；  ④CG⊥AE，
请把你认为正确的结论的序号填在横线上
①②③
①②③
．
我们发现，用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法．请你用等面积法来探究下列两个问题：
（1）如图1是著名的赵爽弦图，由四个全等的直角三角形拼成，请你用它来验证勾股定理；
（2）如图2，在Rt△ABC中，∠ACB=90°，CD是AB边上的高，AC=4，BC=3，求CD的长度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网